题目内容
2.如图1,直线DE上有一点O,过点O在直线DE上方作射线OC.将一直角三角板AOB(∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方.将直角三角板绕着点O按每秒10?的速度逆时针旋转一周,设旋转时间为t秒.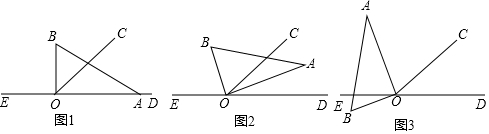
(1)当直角三角板旋转到如图2的位置时,OA恰好平分∠COD,此时,∠BOC与∠BOE之间有何数量关系?并说明理由.
(2)若射线OC的位置保持不变,且∠COE=140°.
①则当旋转时间t=7或25秒时,边AB所在的直线与OC平行?
②在旋转的过程中,是否存在某个时刻,使得射线OA,OC与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值.若不存在,请说明理由.
③在旋转的过程中,当边AB与射线OE相交时(如图3),求∠AOC-∠BOE的值.
分析 (1)由∠AOB=90°知∠BOC+∠AOC=90°、∠AOD+∠BOE=90°,根据∠AOD=∠AOC可得答案;
(2)①由∠COE=140°知∠COD=40°,分AB在直线DE上方和下方两种情况,根据平行线的性质分别求得∠AOD度数,从而求得t的值;
②当OA平分∠COD时∠AOD=∠AOC、当OC平分∠AOD时∠AOC=∠COD、当OD平分∠AOC时∠AOD=∠COD,分别列出关于t的方程,解之可得;
③由∠AOC=∠COE-∠AOE=140°-∠AOE、∠BOE=90°-∠AOE得∠AOC-∠BOE=(140°-∠AOE)-(90°-∠AOE)=50°.
解答 解:(1)∠BOC=∠BOE,
∵∠AOB=90°,
∴∠BOC+∠AOC=90°,∠AOD+∠BOE=90°,
∵OA平分∠COD,
∴∠AOD=∠AOC,
∴∠BOC=∠BOE;
(2)①∵∠COE=140°,
∴∠COD=40°,
如图1,当AB在直线DE上方时,
∵AB∥OC,
∴∠AOC=∠A=30°,
∴∠AOD=∠AOC+∠COD=70°,即t=7;
如图2,当AB在直线DE下方时,
∵AB∥OC,
∴∠COB=∠B=60°,
∴∠BOD=∠BOC-∠COD=20°,
则∠AOD=90°+20°=110°,
∴t=$\frac{360°-110°}{10}$=25,
故答案为:7或25;
②当OA平分∠COD时,∠AOD=∠AOC,即10t=20,解得t=2;
当OC平分∠AOD时,∠AOC=∠COD,即10t-40=40,解得t=8;
当OD平分∠AOC时,∠AOD=∠COD,即360-10t=40,解得:t=32;
综上,t的值为2、8、32;
③∵∠AOC=∠COE-∠AOE=140°-∠AOE,∠BOE=90°-∠AOE,
∴∠AOC-∠BOE=(140°-∠AOE)-(90°-∠AOE)=50°,
∴∠AOC-∠BOE的值为50°.
点评 本题主要考查平行线的性质、角平分线的性质、余角的性质及角的计算,根据题意全面考虑所有可能以分类讨论是解题的关键.

| A. | $\root{3}{-27}$ | B. | -$\frac{5}{3}$ | C. | $\sqrt{0.01}$ | D. | 2π |
| A. | $\frac{x^2}{x^6}=\frac{1}{x^3}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$=a+b | ||
| C. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | D. | $\frac{x+1}{{x}^{2}-2x+1}$=$\frac{1}{x+1}$ |
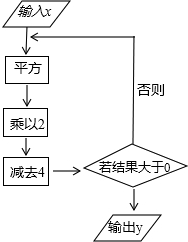 根据如图所示的程序计算.
根据如图所示的程序计算.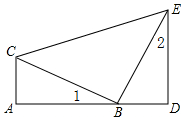 如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2.
如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2. 如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值.
如图,已知在等腰直角三角形ABC中,∠CAB=90°,以AB为边向外作等边△ABD,AE⊥BD,CD、AE交于点M,若DM=1,求BC的值. 如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.
如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.