题目内容
17. 如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.
如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.(1)求证:∠BEF=∠BGD;
(2)求证:DE=DG;
(3)BC与EG垂直吗?为什么?
分析 (1)根据垂直的定义和同角的余角相等即可得到结论;
(2)首先根据等腰三角形的知识得到CD=BD,进而证明出△ECD≌△GBD,于是结论得证;
(3)延长BC交EG于H,求出∠BHD=90°即可证明.
解答 证明:(1)∵AC=BC,点D为AB中点,
∴∠BDG=∠EDG=90°
∴∠BGD+∠DBG=90°,
∵BF⊥EC,
∴∠BEF+∠DBG=90°,
∴∠BEF=∠BGD.
(2)∵AC=BC,∠ACB=90°,
∴∠ABC=∠CAB=45°,
∵∠BDG=90°,
∴∠BCD=90°-∠ABC=45°,
∴∠BCD=∠ABC,
∴CD=BD,
在△ECD和△GBD中$\left\{\begin{array}{l}∠BEF=∠BGD\\ DC=DB\\∠EDC=∠GDB\end{array}\right.$,
∴△ECD≌△GBD,
∴DE=DG;
(3)BC⊥EG,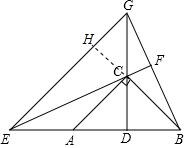
证明:延长BC交EG于H
∵∠EDG=90°,DE=DG,
∴∠DEG=∠DGE=45°,
∴∠BHG=∠DEG+∠ABC=90°,
∴BC⊥EG.
点评 本题主要考查了全等三角形的判定与性质以及等腰三角形的知识,解(1)要掌握同角的余角相等,解(2)关键是证明△ECD≌△GBD,解(3)关键是作辅助性.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
8.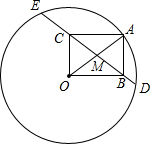 如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )
如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )
 如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )
如图,⊙O的半径为10,A是⊙O上一点.以OA为对角线作矩形OBAC,且OC=6.延长BC,与⊙O分别交于D,E两点,则△OCE和△OBD的周长差等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | 1 | D. | $\frac{6}{5}$ |
5. 如图,PA,PB分别切⊙O于A,B,∠APB=60°,PA=8,则⊙O的半径OA长为( )
如图,PA,PB分别切⊙O于A,B,∠APB=60°,PA=8,则⊙O的半径OA长为( )
 如图,PA,PB分别切⊙O于A,B,∠APB=60°,PA=8,则⊙O的半径OA长为( )
如图,PA,PB分别切⊙O于A,B,∠APB=60°,PA=8,则⊙O的半径OA长为( )| A. | 4 | B. | 8 | C. | $\frac{4}{3}$$\sqrt{3}$ | D. | $\frac{8}{3}$$\sqrt{3}$ |
12.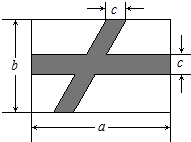 如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )
如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )
 如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )
如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )| A. | ab-bc-ac+c2 | B. | bc-ab+ac | C. | b2-bc+a2-ab | D. | a2+ab+bc-ac |
3.(1+3a)(3a-1)=( )
| A. | 3a2-1 | B. | 1-9a2 | C. | 9a2-1 | D. | a2-3 |
4.下列各数中,为负数的是( )
| A. | 0 | B. | -2 | C. | 1 | D. | 0.001 |
 如图,边长都为1的正方形AEFG与正方形ABCD,正方形AEFG绕顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值为1和2.
如图,边长都为1的正方形AEFG与正方形ABCD,正方形AEFG绕顶点A旋转一周,在此旋转过程中,线段DF的长可取的整数值为1和2.