题目内容
当x 时,分式
有意义;当x 时,分式
的值为零.
| x2-4 |
| x-2 |
| x2-4 |
| x-2 |
考点:分式的值为零的条件,分式有意义的条件
专题:
分析:(1)分式
有意义的条件为x-2≠0,即可解得x的范围;
(2)要使分式的值为0,必须分式分子的值为0并且分母的值不为0.
| x2-4 |
| x-2 |
(2)要使分式的值为0,必须分式分子的值为0并且分母的值不为0.
解答:解:根据题意得:x-2≠0,即x≠2;
由分子x2-4=0解得:x=±2.
而x-2≠0,x≠2
所以x=-2.
故答案为:≠2;=-2.
由分子x2-4=0解得:x=±2.
而x-2≠0,x≠2
所以x=-2.
故答案为:≠2;=-2.
点评:此题主要考查了分式的意义以及分式的值为0,要求掌握.意义:对于任意一个分式,分母都不能为0,否则分式无意义.
解此类问题,只要令分式中分母不等于0,求得字母的取值即可.
若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
解此类问题,只要令分式中分母不等于0,求得字母的取值即可.
若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.

练习册系列答案
相关题目

 观察下面有※组成的图案和算式:
观察下面有※组成的图案和算式: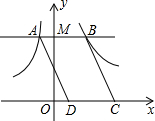 如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-
如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-