题目内容
如图1,ABCD是边长为1的正方形,O是正方形的中心,Q是边CD上一个动点(点Q不与点C、D重合),直线AQ与BC的延长线交于点E,AE交BD于点P.设DQ=x.

(1)填空:当x=
时,
的值为 ;
(2)如图2,直线EO交AB于点G,若BG=y,求y关于x之间的函数关系式;
(3)在第(2)小题的条件下,是否存在点Q,使得PG∥BC?若存在,求x的值;若不存在,说明理由.

(1)填空:当x=
| 2 |
| 3 |
| AP |
| EQ |
(2)如图2,直线EO交AB于点G,若BG=y,求y关于x之间的函数关系式;
(3)在第(2)小题的条件下,是否存在点Q,使得PG∥BC?若存在,求x的值;若不存在,说明理由.
考点:相似三角形的判定与性质,正方形的性质
专题:几何综合题
分析:(1)先根据平行线分相等成比例定理得出
=
=
,
=
,然后根据已知条件求得CE=
,进而求得QE=
AE,AP=
AE后即可求得;
(2)过O作OM⊥AB,ON⊥BC,根据平行线分相等成比例定理得出CE=
,进而求得BE=
,然后根据
=
,即可求得解析式;
(3)根据PG∥BC求得
=
=
,根据对应边成比例得出y=
,再根据(2)中求得的解析式解方程组,即可求得.
| AD |
| CE |
| DQ |
| QC |
| AQ |
| QE |
| AD |
| BE |
| AP |
| PE |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 5 |
(2)过O作OM⊥AB,ON⊥BC,根据平行线分相等成比例定理得出CE=
| 1-x |
| x |
| 1 |
| x |
| GM |
| GB |
| OM |
| BE |
(3)根据PG∥BC求得
| AG |
| GB |
| AP |
| PE |
| AD |
| BE |
| 1 |
| x+1 |
解答: 解:(1)∵ABCD是边长为1的正方形,
解:(1)∵ABCD是边长为1的正方形,
∴AD∥BE,
∴
=
=
,
=
,
∵AD=BC=DC=1,DQ=
,
∴QC=
,
∴
=
,
∴CE=
,
=
,
∴BE=
,QE=
AE,
∴
=
,即
=
,
∴AP=
AE,
∴
=
=
;
 (2)过O作OM⊥AB,ON⊥BC,
(2)过O作OM⊥AB,ON⊥BC,
∵O是正方形的中心,
∴OM=MB=BN=ON=
,
∵
=
,
∴
=
,
∴CE=
,
∴BE=BC+EC=
,
∵OM∥BE,
∴△GMO∽△GBE,
∴
=
,
即
=
,整理得:(2-x)y=1,
∴y=
,
∴y关于x之间的函数关系式为y=
;
(3)存在;
理由:∵PG∥BC,
∴
=
=
,
∵AG=1-y,GB=y,AD=1,BE=
,
∴
=
,整理得:y=
,
解
得x=
,
所以当x=
时,使得PG∥BC.
 解:(1)∵ABCD是边长为1的正方形,
解:(1)∵ABCD是边长为1的正方形,∴AD∥BE,
∴
| AD |
| CE |
| DQ |
| QC |
| AQ |
| QE |
| AD |
| BE |
| AP |
| PE |
∵AD=BC=DC=1,DQ=
| 2 |
| 3 |
∴QC=
| 1 |
| 3 |
∴
| 1 |
| CE |
| ||
|
∴CE=
| 1 |
| 2 |
| AQ |
| QE |
| 2 |
| 1 |
∴BE=
| 3 |
| 2 |
| 1 |
| 3 |
∴
| 1 | ||
|
| AP |
| PE |
| AP |
| PE |
| 2 |
| 3 |
∴AP=
| 2 |
| 5 |
∴
| AP |
| EQ |
| ||
|
| 6 |
| 5 |
 (2)过O作OM⊥AB,ON⊥BC,
(2)过O作OM⊥AB,ON⊥BC,∵O是正方形的中心,
∴OM=MB=BN=ON=
| 1 |
| 2 |
∵
| AD |
| CE |
| DQ |
| QC |
∴
| 1 |
| CE |
| x |
| 1-x |
∴CE=
| 1-x |
| x |
∴BE=BC+EC=
| 1 |
| x |
∵OM∥BE,
∴△GMO∽△GBE,
∴
| GM |
| GB |
| OM |
| BE |
即
y-
| ||
| y |
| ||
|
∴y=
| 1 |
| 2-x |
∴y关于x之间的函数关系式为y=
| 1 |
| 2-x |
(3)存在;
理由:∵PG∥BC,
∴
| AG |
| GB |
| AP |
| PE |
| AD |
| BE |
∵AG=1-y,GB=y,AD=1,BE=
| 1 |
| x |
∴
| 1-y |
| y |
| 1 | ||
|
| 1 |
| x+1 |
解
|
| 1 |
| 2 |
所以当x=
| 1 |
| 2 |
点评:本题考查了三角形相似的判定和性质、平行线分相等定理的应用、正方形的性质等,找出对应线段之间的关系是本题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
下列说法正确的是( )
| A、两条对角线相等的四边形是平行四边形 |
| B、两条对角线相等且互相垂直的四边形是矩形 |
| C、两条对角线互相垂直平分的四边形是菱形 |
| D、两条对角线平分且相等的四边形是正方形 |
 根据题意结合图形填空:
根据题意结合图形填空: 已知:如图,矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长和矩形的面积.
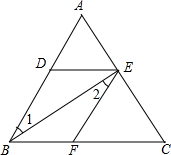
已知:如图,矩形ABCD的两条对角线AC、BD相交于点O,∠AOD=120°,AB=2.5cm.求矩形对角线的长和矩形的面积. 如图,∠1=20°,∠2=25°,∠A=45°,求∠BOC的度数.
如图,∠1=20°,∠2=25°,∠A=45°,求∠BOC的度数. 已知,如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点,
已知,如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点,