题目内容
若直角三角形的两直角边长为a、b,且满足
+|4-b|=0,则该直角三角形的斜边长为 .
| a2-6a+9 |
考点:勾股定理,非负数的性质:绝对值,非负数的性质:算术平方根
专题:
分析:先根据非负数的性质求出两直角边长a、b,已知两直角边求斜边可以根据勾股定理求解.
解答:解:∵
+|4-b|=0,
∴a2-6a+9=0,4-b=0,
解得a=3,b=4,
∴该直角三角形的斜边长为
=5.
故答案为:5.
| a2-6a+9 |
∴a2-6a+9=0,4-b=0,
解得a=3,b=4,
∴该直角三角形的斜边长为
| 32+42 |
故答案为:5.
点评:本题考查了非负数的性质,根据勾股定理计算直角三角形的斜边,正确的运用勾股定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O是△ABC的外接圆,∠OCB=50°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=50°,则∠A的度数等于( )| A、40° | B、50° |
| C、60° | D、70° |
下列四个图形中,∠1和∠2是对顶角的图形有( )


| A、0个 | B、1个 | C、2个 | D、3个 |
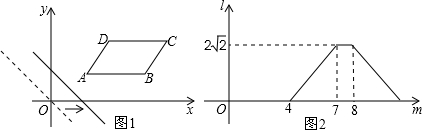
 已知,大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图.大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题:
已知,大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图.大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题: