题目内容
5.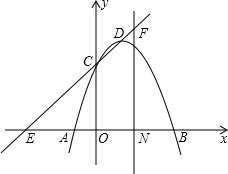 已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.
已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.(1)求抛物线的解析式和点D的坐标;
(2)直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,求NF的长;
(3)在第(2)小题的条件下,直线NF上是否存在点M,使得以点M为圆心、OM为半径的圆与直线CD相切?若存在,求出点M的坐标;若不存在,请说明理由.
分析 (1)设该抛物线的解析式为y=a(x+1)(x-3)(a≠0),把C(0,3)代入该函数解析式可以求得a的值;由抛物线解析式来求其顶点坐标;
(2)设直线CD的解析式为y=kx+b(k≠0),把C、D两点的坐标代入,求出直线CD的解析式;
(3)设存在,作MQ⊥CD于Q,由Rt△FQM∽Rt△FNE,得 $\frac{MQ}{EN}$=$\frac{FM}{EF}$,及可得出关于m的一元二次方程,求出方程的解,即可得出点M的坐标.
解答 解:(1)设该抛物线的解析式为y=a(x+1)(x-3)(a≠0),把C(0,3)代入,得
3=a(0+1)(0-3),
解得a=-1,
则该抛物线解析说法为:y=-(x+1)(x-3)=-x2+2x+3.
当x=-$\frac{2}{2×(-1)}$=1时,y=4.
所以点D的坐标是(1,4);
(2)设直线CD的解析式为y=kx+b(k≠0),把C(0,3),D(1,4)代入,得
$\left\{\begin{array}{l}{b=3}\\{k+b=4}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{b=3}\\{k=1}\end{array}\right.$,
∴直线CD的解析式为y=x+3,
∴E(-3,0),
∴OE=OC=3,
∴∠AEC=45°.
∵点N是OB的中点,
∴ON=$\frac{3}{2}$,NE=$\frac{9}{2}$.
∵FN⊥x轴,
∴∠AEC=∠EFN=45°,
∴NF=EN=$\frac{9}{2}$;
(3)存在.
由(2)得,E(-3,0),
∵点B的坐标(3,0),N是线段OB的中点,
∴N($\frac{3}{2}$,0)
∴F($\frac{3}{2}$,$\frac{9}{2}$),EN=$\frac{9}{2}$,
作MQ⊥CD于Q,
设存在满足条件的点M($\frac{3}{2}$,m),则FM=$\frac{9}{2}$-m,
EF=$\sqrt{(\frac{9}{2})^{2}+({\frac{9}{2})}^{2}}$=$\frac{9\sqrt{2}}{2}$,MQ=OM=$\sqrt{\frac{9}{4}+{m}^{2}}$,由题意得:Rt△FQM∽Rt△FNE,
∴$\frac{MQ}{EN}$=$\frac{FM}{EF}$,
即$\frac{\sqrt{\frac{9}{4}+{m}^{2}}}{\frac{9}{2}}$=$\frac{\frac{9}{2}-m}{\frac{9\sqrt{2}}{2}}$,
∴2($\frac{9}{4}$+m2)=($\frac{9}{2}$-m)2,
整理得4m2+36m-63=0,
∴m2+9m=$\frac{63}{4}$,
m2+9m+$\frac{81}{4}$=$\frac{63}{4}$+$\frac{81}{4}$,
(m+$\frac{9}{2}$)2=$\frac{144}{4}$,
m+$\frac{9}{2}$=±$\frac{12}{2}$,
∴m1=$\frac{3}{2}$,m2=-$\frac{21}{2}$,
∴点M的坐标为M1($\frac{3}{2}$,$\frac{3}{2}$),M2($\frac{3}{2}$,-$\frac{21}{2}$).
点评 本题是二次函数的综合题型,其中涉及的知识点有一元二次方程的解法.在求有关存在不存在问题时要注意先假设存在,再讨论结果.

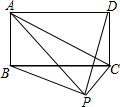 已知矩形ABCD,当点P在图中的位置时,则有结论( )
已知矩形ABCD,当点P在图中的位置时,则有结论( )| A. | S△PBC=S△PAC+S△PCD | B. | S△PBC=S△PAC-S△PCD | ||
| C. | S△PAB+S△PCD=$\frac{1}{2}$S矩形ABCD | D. | S△PAB+S△PCD<$\frac{1}{2}$S矩形ABCD |
| 距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
| 温度(℃) | 20 | 14 | 8 | 2 | -4 | -10 |
(1)如果用h(单位:km)表示距离地面的高度,用T(单位:℃)表示温度,T如何随着h的变化而变化?写出T随着h随着h变化的函数解析式;
(2)画出函数图象;
(3)你能预测出距离地面6km的高空温度是多少吗?
| A. | x≠2 | B. | x≥2 | C. | x>2 | D. | x≥-2 |
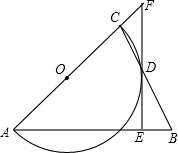 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.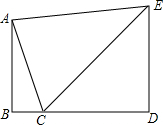 如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线.
如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线. 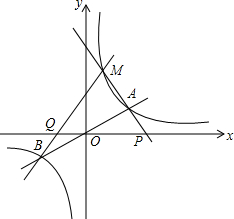 如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.