题目内容
17.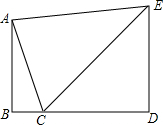 如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线.
如图,小明想利用自己所学的数学知识测量连接塔AB的尖端和地面间的一条空中速滑索道AC的长度,小明先测得塔尖A在点C的北偏西22°方向,然后沿坡比为1:1(即tan∠ECD=1)的斜坡以18/分的速度步行2分钟到达E,测得点A的俯角为8°,若点A、B、C、D、E,都在同一平面内,且B、C、D三点共线. (1)求索道AC的长度;
(2)求点A与点E间的距离.
(参考数据:sin76°≈$\frac{24}{25}$,cos76°≈$\frac{6}{25}$,tan76°≈4,sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
分析 (1)根据速度乘以时间得出CE的长度,通过坡度得到∠ECD=45°,作辅助线CF⊥AE于F,EG∥BD,解直角△CEF,求出CF与EF的长,再解直角△CAF,可求出AF及索道AC的长度;
(2)根据AE=AF+EF即可求出点A与点E间的距离.
解答 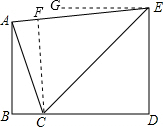 解:(1)作CF⊥AE于F,EG∥BD,则∠CEG=∠ECD.
解:(1)作CF⊥AE于F,EG∥BD,则∠CEG=∠ECD.
根据题意,CE=18×2=36,∠GEA=8°.
∵tan∠ECD=1,
∴∠ECD=∠CEG=45°,
∵∠AEC=45°-8°=37°.
在直角△CEF中,∵∠CFE=90°,∠CEF=37°,CE=36,
∴CF=CE•sin∠CEF≈36×$\frac{3}{5}$=21.6,EF=CE•cos∠CEF≈36×$\frac{4}{5}$=28.8.
∵∠ACB=90°-22°=68°,∠ECD=45°,
∴∠ACE=180°-68°-45°=67°,
∴∠CAE=180°-∠ACE-∠AEC=180°-67°-37°=76°.
在直角△CAF中,∵∠CFA=90°,∠CAF=76°,CF≈21.6,
∴AF=$\frac{CF}{tan∠CAF}$≈$\frac{21.6}{4}$=5.4,AC=$\frac{CF}{sin∠CAF}$≈$\frac{21.6}{\frac{24}{25}}$=22.5;
(2)由(1)知AF≈5.4,EF≈28.8,
则AE=AF+EF≈5.4+28.8=34.2.
点评 本题考查了解直角三角形的应用-方向角问题,解直角三角形的应用-坡度坡角问题,解答本题的关键是作辅助线CF⊥AE于F构造直角三角形.

练习册系列答案
相关题目
9.对某条路线的长度进行5次测量,得到5个结果(单位:km):x1=104,x2=101,x3=102,x4=104,x5=103.如果用x作为这条路线长度的近似值,要使得(x-x1)2+(x-x2)2+…+(x-x5)2的值最小,x应选取这5次测量结果的( )
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 最小值 |
8.∠1与∠2互余,∠1与∠3互补,若∠3=125°,则∠2=( )
| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
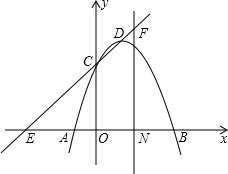 已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.
已知抛物线经过A(-1,)、B(3,0),C(0,3),点D为抛物线的顶点.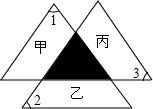 如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )
如图的灰色小三角形为三个全等大三角形的重迭处,且三个大三角形各扣掉灰色小三角形后分别为甲、乙、丙三个梯形.若图中标示的∠1为58°,∠2为62°,∠3为60°,则关于甲、乙、丙三梯形的高的大小关系,下列叙述何者正确?( )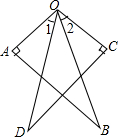 如图,OA⊥AB,OC⊥CD,OA=OC,OB=OD,求证:∠1=∠2.
如图,OA⊥AB,OC⊥CD,OA=OC,OB=OD,求证:∠1=∠2.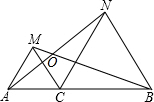 如图,C为线段AB上一点,△ACM,△CBN是等边三角形,且AN,BN相交于点O.
如图,C为线段AB上一点,△ACM,△CBN是等边三角形,且AN,BN相交于点O. 尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.
尼泊尔地震牵动着全中国人民的心,中国红十字基金会开展了“一方有难,八方支援”的赈灾活动.5月15日,中国红十字基金会联手北京成龙慈善基金会等共同出资400万元人民币,采购5000只“赈济家庭箱”(“赈济家庭箱”包括当地受灾群众急需的毛毯、防潮垫、睡袋、雨衣、服装、餐具、个人护理用品等),作为首批物资援助尼泊尔地震灾区.该基金会计划到第三批援助物资为止共采购18200只“赈济家庭箱”.