题目内容
一个圆锥的侧面展开图形是一个半径为6cm的半圆，则这个圆锥的全面积是 ．
考点：圆锥的计算
专题：
分析：首先利用圆的面积公式求得侧面积，利用弧长公式求得圆锥的底面半径，得到底面面积，据此即可求得圆锥的全面积．
解答：解：侧面积是：
×π×62=18π．
设圆锥的底面半径是rcm，半径为6cm的半圆的弧长是6πcm，
则得到2πr=6π，
解得：r=3，
底面积=π×32=9π．
故圆锥的全面积是：18π+9π=27π（cm2）．
故答案是：27πcm2．
| 1 |
| 2 |
设圆锥的底面半径是rcm，半径为6cm的半圆的弧长是6πcm，
则得到2πr=6π，
解得：r=3，
底面积=π×32=9π．
故圆锥的全面积是：18π+9π=27π（cm2）．
故答案是：27πcm2．
点评：本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长等于侧面展开图的扇形半径；圆锥的底面周长等于侧面展开图的扇形弧长．
练习册系列答案
相关题目
已知线段a（如图），把它六等分．
如图在长度为1个单位长度的小正方形组成的正方形中，点A，B，C在小正方形的顶点上．画出关于l成轴对称图形的△AB′C，五边形ACBB′C′的周长为
如图，AB=AC，点D为BC的中点，∠BDE=∠CDF，DE、DF分别与CA、BA的延长线交于点E、F，求证：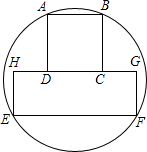
已知正方形ABCD和矩形EFGH按如图位置摆放，且AD=EH=2，EF=4，一圆过A，B，F，E四点，求该圆半径的长．
（1）如图，已知点C在线段AB上，且AC=8cm，BC=6cm，点M、N分别是AC、BC的中点，求线段MN的长度．