题目内容
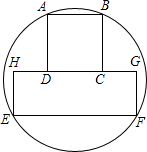 已知正方形ABCD和矩形EFGH按如图位置摆放,且AD=EH=2,EF=4,一圆过A,B,F,E四点,求该圆半径的长.
已知正方形ABCD和矩形EFGH按如图位置摆放,且AD=EH=2,EF=4,一圆过A,B,F,E四点,求该圆半径的长.考点:垂径定理,勾股定理
专题:
分析:延长BC交EF于M,交圆于N,连接AN,根据圆周角定理可知AN是⊙O的直径,AB∥EF可知,圆心必在AB、EF的中点所在的直线上,故可得出EN与MF的长,再根据相交弦定理求出MN的长,根据勾股定理即可得出AN的长,进而得出结论.
解答: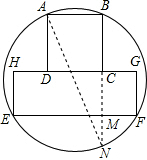 解:延长BC交EF于M,交圆于N,连接AN,
解:延长BC交EF于M,交圆于N,连接AN,
∵AB∥EF
∴圆心必在AB、EF的中点所在的直线上,
∵AB=2,EF=4,
∴MF=1,EM=3,BM=AD+EH=4
∴EM•MF=BM•MN,即3×1=4MN,解得MN=
,
∴BN=BM+MN=4+
=
.
在Rt△ABN中,
∵AB=2,BN=
,
∴AN=
=
=
,
∴圆的半径为
.
 解:延长BC交EF于M,交圆于N,连接AN,
解:延长BC交EF于M,交圆于N,连接AN,∵AB∥EF
∴圆心必在AB、EF的中点所在的直线上,
∵AB=2,EF=4,
∴MF=1,EM=3,BM=AD+EH=4
∴EM•MF=BM•MN,即3×1=4MN,解得MN=
| 3 |
| 4 |
∴BN=BM+MN=4+
| 3 |
| 4 |
| 19 |
| 4 |
在Rt△ABN中,
∵AB=2,BN=
| 19 |
| 4 |
∴AN=
| AB2+BN2 |
22+(
|
5
| ||
| 4 |
∴圆的半径为
5
| ||
| 8 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
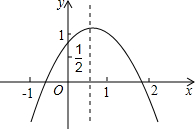 抛物线y=ax2+bx+c的图象如图所示,下列结论正确的是( )
抛物线y=ax2+bx+c的图象如图所示,下列结论正确的是( )| A、abc>0 |
| B、a+c>0 |
| C、b2+4a>4ac |
| D、2a+b>0 |
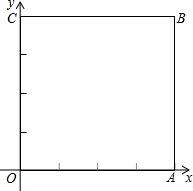 如图,已知正方形OABC的边长为4,请写出各个顶点的坐标.如果将它们的坐标同时缩小一半,得到一组新坐标,画出新坐标所对应的点,并把他们连接起来,得到一个新的图形,说出它的名称,你能说明其中的道理吗?
如图,已知正方形OABC的边长为4,请写出各个顶点的坐标.如果将它们的坐标同时缩小一半,得到一组新坐标,画出新坐标所对应的点,并把他们连接起来,得到一个新的图形,说出它的名称,你能说明其中的道理吗?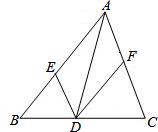 已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.
已知△ABC,DE∥AC交AB于E,DF∥AB交AC于F.