题目内容
一次函数 y=kx+b(k≠0)满足﹣4≤x≤1 时,﹣2≤y≤2,则一次函数解析式为
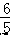 y=
y=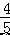 x+
x+ 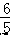 或 y=﹣
或 y=﹣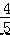 x -
x -
【考点】待定系数法求一次函数解析式.
【分析】分类讨论:由于一次函数是递增或递减函数,所以当一次函数 y=kx+b 为增函数时,则 x=
﹣4,y=﹣2;x=1,y=2;当一次函数 y=kx+b 为减函数时,则 x=﹣4,y=2;x=1,y=﹣2,然后把它 们分别代入 y=kx+b 中得到方程组,再解两个方程组即可.
【解答】解:当一次函数 y=kx+b 为增函数时,
∵﹣4≤x≤1 时,﹣2≤y≤2,
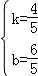 ∴x=﹣4,y=
∴x=﹣4,y= ﹣2;x=1,y=2,
﹣2;x=1,y=2,
∴ 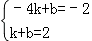 ,解得 ,
,解得 ,
∴一次函数的解析式为 y=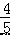 x+
x+ 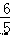 ; 当一次函数 y=kx+b 为减函数时,
; 当一次函数 y=kx+b 为减函数时,
∵﹣4≤x≤1 时,﹣2≤y≤2,
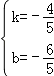 ∴x=﹣4,y=2;x=1,y=﹣2,
∴x=﹣4,y=2;x=1,y=﹣2,
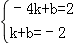 ∴ ,解得 ,
∴ ,解得 ,
∴一次函数的解析式为 y=﹣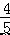 x﹣
x﹣ 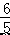 . 综上所述,一次函数解析式为 y=
. 综上所述,一次函数解析式为 y=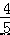 x+
x+ 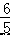 或 y=﹣
或 y=﹣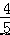 x﹣
x﹣ 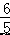 . 故答案为:y=
. 故答案为:y= 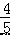 x+
x+ 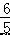 或 y=﹣
或 y=﹣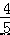 x﹣
x﹣ 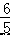 .
.
【点评】本题考查的是待定系数法求一次函数的解析式,先根据题意判断出一次函数的增减性是解
答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
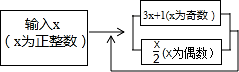
 = .
= .
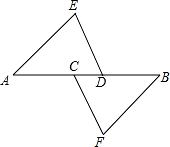
 ∠A=40°,求∠DBC 的度数.
∠A=40°,求∠DBC 的度数.