题目内容
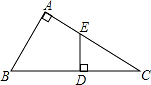
如图,△ABC 中,AB=AC=5,AB 的垂直平分线 DE 交 AB、AC 于 E、D.
(1)若△BCD 的周长为 8,求 BC 的长; 若 ∠A=40°,求∠DBC 的度数.
∠A=40°,求∠DBC 的度数.
【考点】线段垂直平分线的性质;等腰三角形的性质.
【分析】(1)根据线段垂直平 分线定理得出 AD=BD,根据 BC+CD+BD=8cm 求出 AC+BC=8cm,把 AC 的长代入求出即可;
分线定理得出 AD=BD,根据 BC+CD+BD=8cm 求出 AC+BC=8cm,把 AC 的长代入求出即可;
已知∠A=40°,AB=AC 可得∠ABC=∠ACB,再由线段垂直平分线的性质可求出∠ABC=∠A,易求
∠DBC.
【解答】解:(1)∵D 在 AB 垂直平分线上,
∴AD=BD,
∵△BCD 的周长为 8cm,
∴BC+CD+BD=8cm,
∴AD+DC+BC=8cm,
∴AC+BC=8cm,
∵AB=AC=5cm,
∴BC=8cm﹣5 cm=3cm;
cm=3cm;
∵∠A=40°,AB=AC,
∴∠ABC=∠ACB=70°,
又∵DE 垂直平分 AB,
∴DB=AD
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°.
【点评】本题考查了等腰三角形性质和线段垂直平分线定理,关键是求出 AC+BC 的值,注意:线 段垂直平分线上的点到线段的两端点的距离相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
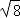 +
+ 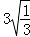 ﹣
﹣ 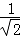 +
+ 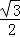 ;
;
 是平行四边形,下列结论中不正确的是( ).
是平行四边形,下列结论中不正确的是( ). 时,它是菱形 B.当
时,它是菱形 B.当 时,它是菱形
时,它是菱形 C.当
C.当 时,它是矩形 D. 当
时,它是矩形 D. 当 时,它是正方形
时,它是正方形