题目内容
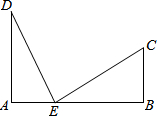 某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?
某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方?考点:勾股定理的应用
专题:
分析:设AE=x千米,则BE=(25-x)千米,再根据勾股定理得出DA2+AE2=BE2+BC2,进而可得出结论.
解答:解:设AE=x千米,则BE=(25-x)千米,
在Rt△DAE中,DA2+AE2=DE2,
在Rt△EBC中,BE2+BC2=CE2,
∵CE=DE,
∴DA2+AE2=BE2+BC2,
∴152+x2=102+(25-x)2,
解得,x=10千米.
答:基地应建在离A站10千米的地方.
在Rt△DAE中,DA2+AE2=DE2,
在Rt△EBC中,BE2+BC2=CE2,
∵CE=DE,
∴DA2+AE2=BE2+BC2,
∴152+x2=102+(25-x)2,
解得,x=10千米.
答:基地应建在离A站10千米的地方.
点评:本题考查的是勾股定理的应用,熟知勾股定理是解答此题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
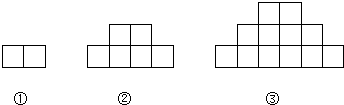
如图,第①个图有2个相同的小正方形,第②个图有6个相同的小正方形,第③个图有12个相同的小正方形,…,按此规律,那么第15个图中小正方形的个数是( )

| A、225 | B、240 |
| C、30 | D、255 |
 如图,EG∥AB,FG∥DC,∠B=100°,∠C=120°,∠EGF的度数是( )
如图,EG∥AB,FG∥DC,∠B=100°,∠C=120°,∠EGF的度数是( )| A、30° | B、40° |
| C、45° | D、60° |


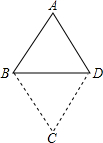 如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题: 如图,与∠1是同位角的角是
如图,与∠1是同位角的角是