题目内容
19. 如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP,此时DP+CP=DP+PC′=DC′的值最小.由DC=1,BC=4,得到BD=3,连接BC′,由对称性可知∠C′BA=∠CBA=45°,于是得到∠CBC′=90°,然后根据勾股定理即可得到结论.
解答 解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.
此时DP+CP=DP+PC′=DC′的值最小.
∵ BD=3,DC=1
BD=3,DC=1
∴BC=4,
∴BD=3,
连接BC′,由对称性可知∠C′BA=∠CBA=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=4,
根据勾股定理可得DC′=$\sqrt{BC{′}^{2}+B{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故选B.
点评 此题考查了轴对称-线路最短的问题,确定动点P何位置时,使PC+PD的值最小是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
 如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,且AD=6cm,CD=8cm,P是AB上的动点,PM⊥AC于M,PN⊥BD于N,则PM+PN的值为( )| A. | $\frac{24}{5}$cm | B. | 4cm | C. | 5cm | D. | $\frac{13}{5}$cm |




 如图,AB∥CD,点E在AB上,点F在CD上,连接EF,FG平分∠CFE交AB于点G,.若∠FEB=140°,求∠FGE的度数.
如图,AB∥CD,点E在AB上,点F在CD上,连接EF,FG平分∠CFE交AB于点G,.若∠FEB=140°,求∠FGE的度数.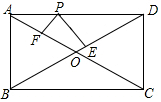 如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( )
如图,矩形ABCD中,已知AD=4,AB=3,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,则PE+PF=( ) 在数轴上作出表示$\sqrt{20}$的点P(要求尺规作图,并保留痕迹).
在数轴上作出表示$\sqrt{20}$的点P(要求尺规作图,并保留痕迹). 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(3a-1,b),则a与b的数量关系为( )
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(3a-1,b),则a与b的数量关系为( )