题目内容
13.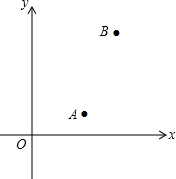 如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).
如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).
分析 作点A关于y轴的对称点A′,连接AA′交y轴于点P,则点C即为所求点;由A点坐标求出A′点坐标,利用待定系数法求出直线A′B的解析式,进而可得出C点坐标.
解答 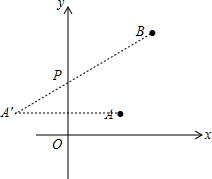 解:如图所示,点P即为所求点.
解:如图所示,点P即为所求点.
∵A(3,1),
∴A′(-3,1),
设直线A′B的解析式为y=kx+b(k≠0),
∵B(5,5),
∴$\left\{\begin{array}{l}{-3k+b=1}\\{5k+b=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{5}{2}}\end{array}\right.$,
∴直线A′B的解析式为y=$\frac{1}{2}$x+$\frac{5}{2}$,
∵当x=0时,y=$\frac{5}{2}$,
∴p(0,$\frac{5}{2}$).
故答案为:(0,$\frac{5}{2}$).
点评 本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
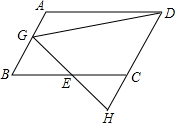 如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.
如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.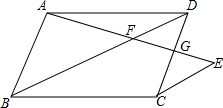 已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.
已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.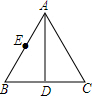 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.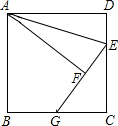 如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.
如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.