题目内容
16.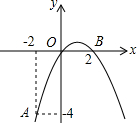 如图,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2、0)三点.
如图,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2、0)三点.(1)求抛物线的解析式;
(2)若点M是抛物线的对称轴上一点,求△AOM周长的最小值.
分析 (1)把A(-2,-4),O(0,0),B(2、0)三点代入抛物线y=ax2+bx+c解方程组即可.
(2)如图,连接AB与对称轴交于点M,此时△AOM周长最小,△AOM周长最小值=OA+AB,求出OA、AB即可.
解答 (1)解:把A(-2,-4),O(0,0),B(2、0)三点代入抛物线y=ax2+bx+c
得$\left\{\begin{array}{l}{c=0}\\{4a+2b+c=0}\\{4a-2b+c=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\\{c=0}\end{array}\right.$,.
故抛物线解析式为y=-$\frac{1}{2}$x2+x.
(2)解:如图,连接AB与对称轴交于点M,此时△AOM周长最小.
∴△AOM周长最小值=AO+OM+AM=BM+AM+AO=AO+AB=$\sqrt{{2}^{2}+{4}^{2}}$+$4\sqrt{2}$=2$\sqrt{5}$+4$\sqrt{2}$.
∴△AOM周长最小值为2$\sqrt{5}$+4$\sqrt{2}$.
点评 本题考查待定系数法确定函数解析式、轴对称-最短问题等知识,解题的关键是利用轴对称准确找到点M的位置,属于中考常考题型.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
4.已知方程组$\left\{\begin{array}{l}{y=x+1}\\{y=2x-3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\end{array}\right.$,直线y=x+1与直线y=2x-3的交点坐标是( )
| A. | (4,5) | B. | (5,4) | C. | (4,0) | D. | (5,0) |
1.代数式2abc,-3x2+x,-$\frac{3}{x}$,2$\frac{1}{3}$中,单项式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.下列事件中,是不可能事件的是( )
| A. | 买一张电影票,座位号是偶数 | B. | 度量三角形的内角和,结果是360° | ||
| C. | 明天会下雨 | D. | 设计运动员射击一次,命中8环 |
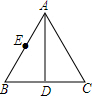 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2,点M是AD上一动点,求△BEM的周长的最小值.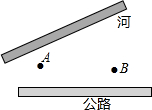 如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.
如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.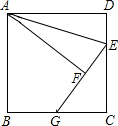 如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.
如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.