题目内容
16.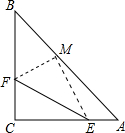 如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.
如图,△ABC中,CA=CB,∠ACB=90°,E、F分别在CA、CB上,将△CEF沿直线EF翻折,点C恰好落在AB上的点M处,若AM=3BM,求$\frac{CF}{CE}$.
分析 过M作MG⊥BC于G,MH⊥AC于H,得到四边形MGCH是矩形,根据矩形的性质得到CH=MG,得到△BMG是等腰直角三角形,通过△AHM∽△BMG,得到$\frac{GM}{MH}=\frac{BM}{AM}$,求得$\frac{CH}{MH}=\frac{BM}{AM}$=$\frac{1}{3}$,由于△ECF∽△MHE,即可得到结论.
解答 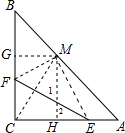 解:过M作MG⊥BC于G,MH⊥AC于H,
解:过M作MG⊥BC于G,MH⊥AC于H,
∵∠ACB=90°,
∴四边形MGCH是矩形,
∴CH=MG,
∵AC=BC,
∴△BMG是等腰直角三角形,
∴BG=GM=CH,
∵MH∥BC,
∴△AHM∽△BMG,
∴$\frac{GM}{MH}=\frac{BM}{AM}$,
∴$\frac{CH}{MH}=\frac{BM}{AM}$=$\frac{1}{3}$,
∵△CEF沿直线EF翻折,点C恰好落在AB上的点M处,
∴EF⊥CM,
∵∠1=∠2,
∴∠HMC=∠CEF,
∴△ECF∽△MHE,
∴$\frac{CF}{CE}=\frac{CH}{HM}$=$\frac{1}{3}$.
点评 本题考查了翻折的性质,相似三角形的判定和性质,等腰直角三角形的性质,矩形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
11.(6x-2y)2•(-xy)-2=( )
| A. | 36x-6 | B. | 36x-3 | C. | -12x-2y4 | D. | -36x-3y |
5.利用二次函数y=x2-2x-2的图象求一元二次方程y=x2-2x-2的近似解时,画图如图1示并进一步估算其中一根列表如下,根据这些信息,可得方程的正的近似根是( )
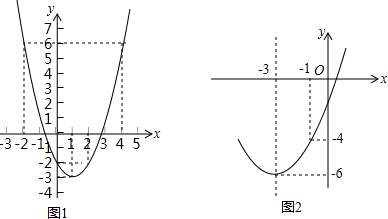
| x | -0.9 | -0.8 | -0.7 | -0.6 |
| y=x2-2x-2 | -0.61 | 0.24 | -0.11 | -0.44 |

| A. | 0.7 | B. | 2.6 | C. | 2.7 | D. | 2.8 |
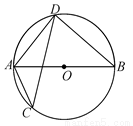
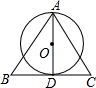 已知:如图.AD是⊙O的直径,直线BC经过点D,并且AB=AC,∠BAD=∠CAD.求证:直线BC是⊙O的切线.
已知:如图.AD是⊙O的直径,直线BC经过点D,并且AB=AC,∠BAD=∠CAD.求证:直线BC是⊙O的切线.