题目内容
把多项式（3a－4b）（7a－8b）＋（11a－12b）（8b－7a）分解因式的结果（ ）
A. 8（7a－8b）（a－b） B. 2（7a－8b）2
C. 8（7a－8b）（b－a） D. －2（7a－8b）
C
【解析】把(3a-4b)(7a-8b)+(11a-12b)(8b-7a)运用提取公因式法因式分解即可得(3a-4b)(7a-8b)+(11a-12b)(8b-7a)
=(7a-8b)(3a-4b-11a+12b)
=(7a-8b)(-8a+8b)
=8(7a-8b)(b-a).
故选：C.
练习册系列答案
备战中考寒假系列答案
相关题目
二次函数y＝x2－(m－4)x－m的图象与x轴的两个交点关于y轴对称，则其顶点坐标为___________．
(0，－4)
【解析】根据二次函数y＝x2－(m－4)x－m的图象与x轴的两个交点关于y轴对称，可知抛物线关于y轴对称，所以 =0，解得m=4，则顶点坐标为（0，-4）．
故答案为：（0，-4）. 已知函数y＝(m2－4)x2＋(m2－3m＋2)x－m－1．
(1)当m为何值时，y是x的二次函数?
(2)当m为何值时，y是x的一次函数?
(1) m≠±2；（2）m＝－2
【解析】试题分析：（1）根据二次函数的概念，二次项的系数不为0，自变量的最高次数为2，求解即可；
（2）根据一次函数的概念，一次项系数不为0，二次项的系数为0，列式求解即可.
试题解析：(1)由m2－4≠0，解得m≠±2．故当m≠±2时，y是x的二次函数．
(2)由m2－4＝0，解得m=±2．由m2－3m＋2≠0，解得m≠1，m≠2．所以m... 先化简，再求值：
已知串联电路的电压U＝IR1+IR2+IR3，当R1＝12.9，R2=18.5，R3=18.6，I=2.3时，求U的值。
115
【解析】试题分析：先根据提取公因式分解U＝IR1+IR2+IR3，再代入求值即可得到结果.
U=I(R1+R2+R3)=2.3×(12.9+18.5+18.6)=2.3×50=115. 观察下列各组整式，其中没有公因式的是( )
A. 2a+b和a+b B. 5m(a-b) 和-a+b
C. 3(a+b) 和-a-b D. 2x+2y和2
A
【解析】选项A，没有公因式；选项B，有公因式a-b；选项C，有公因式a+b；选项D，有公因式2.故选A. 分解因式：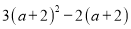 
=______________.
(a+2)(3a+4)
【解析】提取公因式a+2即可，即原式=（a+2）（3a+6-2）=(a+2)(3a+4). 4x2-9=(2x+3)(2x-3)从左到右的变形是__________________.
因式分解
【解析】因式分解是把一个多项式化为几个整式积的形式，由此可得该变形属于因式分解. 已知抛物线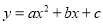
（a＜0）过A（-2，0）、O（0，0）、B（-3， 
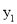）、C（3， 
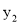）四点，则
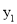与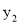
的大小关系是__________
【解析】由已知得抛物线与x轴交于A（-2，0）、O（0，0）两点，开口向下，对称轴为x==-1，可知B（-3， ）、C（3， ）两点在对称轴的两边，点B离对称轴较近，再根据抛物线图象可得．
故答案为： ． 如图，已知抛物线y=﹣x2+bx+c的对称轴为直线x=1，且与x轴的一个交点为（3，0），那么它对应的函数解析式是 ．
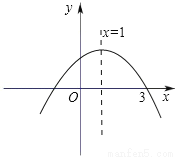
y=﹣x2+2x+3
【解析】
试题分析：∵抛物线y=﹣x2+bx+c的对称轴为直线x=1，
∴=1，解得b=2，
∵与x轴的一个交点为（3，0），
∴0=﹣9+6+c，
解得c=3，
故函数解析式为y=﹣x2+2x+3．
故答案为：y=﹣x2+2x+3