题目内容
先化简，再求值：
已知串联电路的电压U＝IR1+IR2+IR3，当R1＝12.9，R2=18.5，R3=18.6，I=2.3时，求U的值。
115
【解析】试题分析：先根据提取公因式分解U＝IR1+IR2+IR3，再代入求值即可得到结果.
U=I(R1+R2+R3)=2.3×(12.9+18.5+18.6)=2.3×50=115.
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
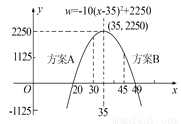
(1)写出商场销售这种工具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；
(2)求销售单价为多少元时，该文具每天的销售利润最大；
(3)商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元．
请比较哪种方案的最大利润更高，并说明理由．
（1）w＝－10x2＋700x－10000；
（2）销售单价为35元时，每天销售利润最大，最大利润为2250元；
（3）方案A的最大利润更高，理由见解析.
【解析】试题分析：（1）根据利润=（销售单价-进价）×销售量，列出函数关系式即可；
（2）根据（1）式列出的函数关系式，运用配方法求最大值；
（3）分别求出方案A、B中x的取值范围，然后分别求出A、B方案的最大利润... 如图，某水渠的横断面是等腰梯形，已知其斜坡AD和BC的坡度为1：0.6，现测得放水前的水面宽EF为1.2米，当水闸放水后，水渠内水面宽GH为2.1米．求放水后水面上升的高度是（ ）
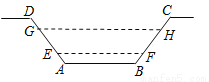
A. 0.55 B. 0.8 C. 0.6 D. 0.75
D
【解析】试题分析：过点E作EM⊥GH，则GM=(2.1-1.2)÷2=0.45米，根据坡度可得：EM=0.45÷0.6=0.75米，故选D． 某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为____．
y＝a(1＋x)2
【解析】试题分析：∵一月份新产品的研发资金为a元，
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为，∴三月份的研发资金为．
故答案为： ． 对于抛物线y＝ax2，下列说法中正确的是（ ）
A. a越大，抛物线开口越大
B. a越小，抛物线开口越大
C. ｜a｜越大，抛物线开口越大
D. ｜a｜越小，抛物线开口越大
D
【解析】试题分析：∵对于y＝ax2图像而言，|a|越小，开口越大
∴D是正确的 把下列各式分解因式：
（1）
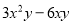（2）
（3）
（4）
（5）
（6）
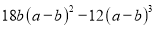
（7）15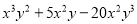
（8）6x(x+y)-4y(x+y)
（9）
（10）
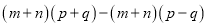
(1)3xy(x-2); (2) ; (3) ; (4) ;
(5) ; (6) ;(7) ;
(8)2(x+y)(3x-2y); (9) ; (10) .
【解析】试题分析：都利用提公因式法分解因式即可.
试题解析：
(1)原式=3xy(x-2);
(2)原式=;
(3)原式=;
(4) ;
(5)原式=;
(6)原式=;
(7)... 把多项式（3a－4b）（7a－8b）＋（11a－12b）（8b－7a）分解因式的结果（ ）
A. 8（7a－8b）（a－b） B. 2（7a－8b）2
C. 8（7a－8b）（b－a） D. －2（7a－8b）
C
【解析】把(3a-4b)(7a-8b)+(11a-12b)(8b-7a)运用提取公因式法因式分解即可得(3a-4b)(7a-8b)+(11a-12b)(8b-7a)
=(7a-8b)(3a-4b-11a+12b)
=(7a-8b)(-8a+8b)
=8(7a-8b)(b-a).
故选：C. 把多项式(m+1)（m-1）+（m-1）分解因式，一个因式是（m-1）,则另一个因式是（ ）
A. m+1 B. 2m C. 2 D. m+2
D
【解析】∵(m+1)（m-1）+（m-1）=（m-1）（m+1+1）=（m-1）（m+2），
∴另一个因式是（m+2）.
故选D. 若y＝ax2＋bx＋c，则由表格中信息可知y与x之间的函数表达式是( )
x | －1 | 0 | 1 |
ax2 | 1 | ||
ax2＋bx＋c | 8 | 3 |
A. y＝x2－4x＋3 B. y＝x2－3x＋4
C. y＝x2－3x＋3 D. y＝x2－4x＋8
A
【解析】把表格中所给的的三对对应值代入对应的式子可得： ，解得： ，
∴与之间的函数表达式为：.
故选A.