题目内容
20.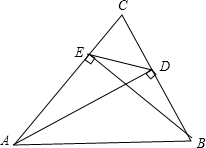 如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.
如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.
分析 根据AD,BE是△ABC的两条高,于是得到∠ADC=∠BEC=90°,由于∠C=∠C,推出△ADC∽△BCE,根据相似三角形的性质得到$\frac{CE}{CD}=\frac{BC}{AC}$,证得△CED∽△ABC,即可得到结论.
解答 证明:∵AD,BE是△ABC的两条高,
∴∠ADC=∠BEC=90°,
∵∠C=∠C,
∴△ADC∽△BCE,
∴$\frac{CE}{CD}=\frac{BC}{AC}$,
∴△CED∽△ABC,
∴∠CED=∠ABC.
点评 本题主要考查了相似三角形的判定和性质,垂直的定义,解决问题的关键是熟记定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
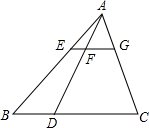 如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.
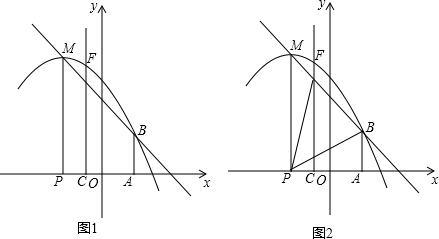
如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.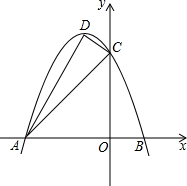 已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.
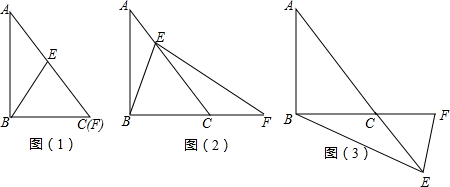
已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.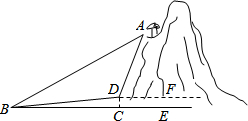 我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.
我市AAAA景区有一处景观奇异的望天洞,D点是望天洞的入口,游人从入口进洞后,可经山洞到山顶的出口亭A处观光,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD的长为120米,坡角为∠DBC=10°,在B出测得A的仰角∠ABC=40°,在D出测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.