题目内容
12.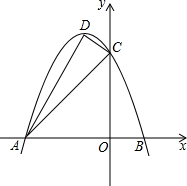 已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.
已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.(1)求抛物线的解析式;
(2)请你判断△ACD的形状,并证明你的结论;
(3)若点Q在抛物线的对称轴上,抛物线上是否存在点P,使得以A、B、Q、P四点为顶点的四边形为平行四边形?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据勾股定理,可得AC,CD,AD的长,根据勾股定理的逆定理,可得答案;
(3)分类讨论:①平行四边形AQBP,根据平行四边形的对角线互相平分,可得答案;
②?ABQP,根据平行四边形的对边相等,可得P点的横坐标,根据自变量与函数值的对应关系,可得P点坐标;
③?ABPQ,根据平行四边形的对边相等,可得P点的横坐标,根据自变量与函数值的对应关系,可得P点坐标.
解答 解:(1)将A、C点坐标代入、及对称轴,得
$\left\{\begin{array}{l}{9a-3b+c=0}\\{c=3}\\{-\frac{b}{2a}=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
抛物线的解析式y=-x2-2x+3;
(2)△ACD是直角三角形,
证明:∵y═-x2-2x+3=-(x-1)2+4,得顶点坐标是(-1,4),
由勾股定理,得
AC2=32+(0-3)2=18,
CD2=(0+1)2+(3-4)2=2,
AD2=(-1+3)2+((4-0)2=20,
AC2+CD2=AD2,
∴△ACD是直角三角形;
(3)①如图1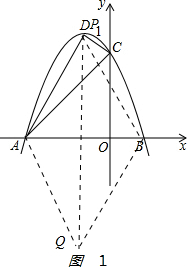 ,平行四边形AQBP,由对角线互相平分,得P1(-1,4),Q(-1,-4);
,平行四边形AQBP,由对角线互相平分,得P1(-1,4),Q(-1,-4);
②如图2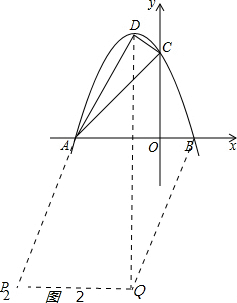 ,
,
?ABQP,PQ=AB=4,-1-4=-5,
当x=-5时,y=-25+10+3=-12,即P2(-5,-12);
③如图3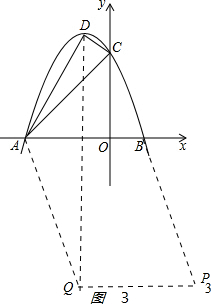 ,
,
?ABPQ,PQ=AB=4,P点的横坐标为-1+4=3,
当x=3时,y=-9-6+3=-12,即P3(3,-12),
综上所述:P1(-1,4),P2(-5,-12),P3(3,-12).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,利用勾股定理、勾股定理的逆定理求三角形的形状;利用平行四边形的性质:对角线互相平分,对边相等是求P点的关键.

 阅读快车系列答案
阅读快车系列答案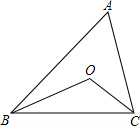 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 115° | B. | 110° | C. | 105° | D. | 130° |
 如图,若干个小正方体搭建的几何体的主视图和俯视图,则搭建的几何体至少用多少个小正方体( )
如图,若干个小正方体搭建的几何体的主视图和俯视图,则搭建的几何体至少用多少个小正方体( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,点C是线段AB的黄金分割点,则下列各式正确的是( )
如图,点C是线段AB的黄金分割点,则下列各式正确的是( )| A. | $\frac{AC}{BC}=\frac{AB}{AC}$ | B. | $\frac{BC}{AB}=\frac{AC}{BC}$ | C. | $\frac{AC}{AB}=\frac{AB}{BC}$ | D. | $\frac{BC}{AB}=\frac{AC}{AB}$ |
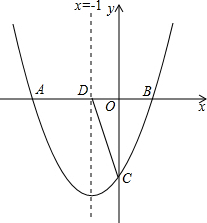 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)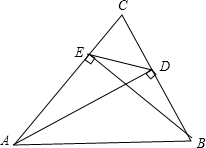 如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.
如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.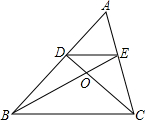 如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7
如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7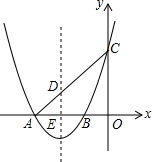 如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.