题目内容
10.已知两条线段的长分别为15cm和25cm,当第三条线段的长为$5\sqrt{34}$或20时,这三条线段可组成一个直角三角形,其面积是$\frac{375}{2}$或150.分析 分两种情况讨论:①第三边作为斜边;②第三边作为直角边;设出第三边的长,利用勾股定理列出方程解之即可.
解答 解:设第三条线段长为x.
①若第三条线段是斜边,则:
152+252=x2,
解得:x=$5\sqrt{34}$,
S=$\frac{1}{2}×15×25$=$\frac{375}{2}$;
②若第三条线段是直角边,则:
152+x2=252,
解得:x=20,
S=$\frac{1}{2}×15×20$=150.
故答案为:$5\sqrt{34}$或20;$\frac{375}{2}$或150.
点评 本题考查勾股定理的基本计算,难度不大.清楚勾股定理的基本内容是解答的关键.要特别注意的是,在题目没告诉哪条边是斜边的情况下,一定要分类讨论,不然就要漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.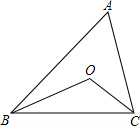 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 115° | B. | 110° | C. | 105° | D. | 130° |
 在如图的长方形纸中,剪出两个圆和一个长方形恰好可以围成一个圆柱,求这个圆柱的体积.
在如图的长方形纸中,剪出两个圆和一个长方形恰好可以围成一个圆柱,求这个圆柱的体积.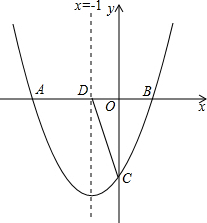 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴交点为A、B两点.其中点A 的坐标为(-3,0)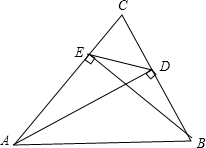 如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.
如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.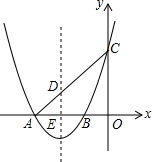 如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.
如图,抛物线y=x2+bx+c交x轴于A(-3,0),B(-1,0)两点,交y轴于点C.已知一次函数y=kx+b的图象过点A,C.