题目内容
14.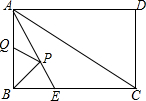 矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )
矩形ABCD中,AB=3,BC=4,∠BAC的平分线交BC于E,P、Q分别是AE、AB上的动点,则PB+PQ的最小值是( )| A. | 5 | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
分析 过B作BH⊥AC于H,交AE于P,过P作PQ⊥AB于Q,于是得到BH即为PB+PQ的最小值,由勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,根据三角形的面积公式得到BH=$\frac{AB•BC}{AC}$=$\frac{12}{5}$,即可得到结论.
解答 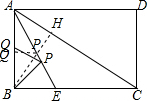 解:过B作BH⊥AC于H,交AE于P,过P作PQ⊥AB于Q,
解:过B作BH⊥AC于H,交AE于P,过P作PQ⊥AB于Q,
∵AE平分∠BAC,
∴PH=PQ,
∴BH=PB+PH=PB+PQ,
则BH即为PB+PQ的最小值,
∵矩形ABCD中,AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∴S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BH,
∴BH=$\frac{AB•BC}{AC}$=$\frac{12}{5}$,
∴PB+PQ的最小值是$\frac{12}{5}$.
点评 本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
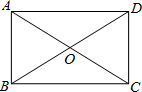 如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$.
如图,矩形ABCD中,对角线AC和BD相交于点0,OD=AD,则sin∠OBA=$\frac{1}{2}$. 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC.
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在AD边上,且AE=DF,AF=CD.求证:FE=FC. 如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.
如图,过?ABCD的对角线的交点O任意作一条直线交AB,CD分别于点E,F.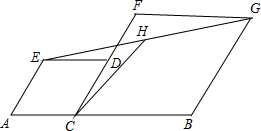 如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.
如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.