题目内容
2.已知不等式$\frac{a-x}{3}$>1的每一个解都是$\frac{2x-1}{2}$<$\frac{1}{2}$的解,则a的取值范围是a≤4.分析 先把a看作常数求出两个不等式的解集,再根据同小取小列出不等式求解即可.
解答 解:解不等式$\frac{a-x}{3}$>1得:x<a-3;
解不等式$\frac{2x-1}{2}$<$\frac{1}{2}$得:x<1,
因为不等式$\frac{a-x}{3}$>1的每一个解都是$\frac{2x-1}{2}$<$\frac{1}{2}$的解,
可得a-3≤1,
解得:a≤4.
故答案为:a≤4
点评 本题考查了解一元一次不等式,分别求出两个不等式的解集,再根据同小取小列出关于a的不等式是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
12.正六边形的中心到边的距离为$\sqrt{3}$,则该正六边形的面积是( )
| A. | 6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 6 | D. | 12 |
13.若9x2+18x+m2是完全平方式,则m的值是( )
| A. | 9 | B. | -3 | C. | 3 | D. | ±3 |
11.做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的高与底面直径的比是( )
| A. | $\frac{a}{b}$ | B. | $\frac{{a}^{2}}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{{b}^{2}}{a}$ |
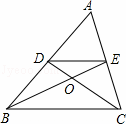 如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,则OC=( )
如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,则OC=( ) 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,请根据图象提供的信息完成下列问题:
甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,请根据图象提供的信息完成下列问题: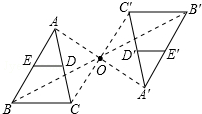 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知BC=6,则E′D′=3.
如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知BC=6,则E′D′=3.