题目内容
12．
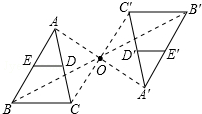如图，△ABC以点O为旋转中心，旋转180°后得到△A′B′C′．ED是△ABC的中位线，经旋转后为线段E′D′．已知BC=6，则E′D′=3．
分析 如图，首先运用旋转的性质判断出△ABC≌△A′B′C′，求出B′C′的长度；运用三角形的中位线定理求出D′E′的长度，即可解决问题．
解答 解：如图，由旋转变换的性质得：
△ABC≌△A′B′C′，
∴B′C′=BC=6；
∵D′E′为△A′B′C′的中位线，
∴E′D′=$\frac{1}{2}$B′C′=3，
故答案为3．
点评 该题主要考查了旋转的性质、三角形的中位线定理等几何知识点及其应用问题；解题的关键是灵活运用旋转的性质、三角形的中位线定理等几何知识点来分析、判断、推理或解答．
练习册系列答案
名校课堂系列答案
相关题目
20．
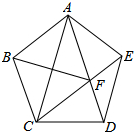如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，已知AB=1，则DF的长是（ ）
如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，已知AB=1，则DF的长是（ ）| A． | $\frac{\sqrt{5}+1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
4．
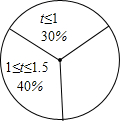为了了解某初级中学800名学生完成课外作业所用的时间情况，从该校学生中随机抽取部分学生进行调查，按被调查学生完成课外作业时间t（小时）的人数分布，制成如图统计表和扇形统计图（均不完整）
根据上述信息，解答下列问题：
（1）抽样的学生数是50 人．在扇形统计图中，当1.5＜t≤2时，
所对的圆心角的度数是72度；
（2）补全统计表与扇形统计图；
（3）若规定，初级中学学生完成课外作业时间不超过1.5小时．根据抽样情况，估计该校学生完成课外作业时间超过规定时间的学生人数．
为了了解某初级中学800名学生完成课外作业所用的时间情况，从该校学生中随机抽取部分学生进行调查，按被调查学生完成课外作业时间t（小时）的人数分布，制成如图统计表和扇形统计图（均不完整）| 时间t（小时） | t≤1 | 1＜t≤1.5 | 1.5＜t≤2 | t＞2 |
| 人数（人） | 15 | 20 | 10 | 5 |
（1）抽样的学生数是50 人．在扇形统计图中，当1.5＜t≤2时，
所对的圆心角的度数是72度；
（2）补全统计表与扇形统计图；
（3）若规定，初级中学学生完成课外作业时间不超过1.5小时．根据抽样情况，估计该校学生完成课外作业时间超过规定时间的学生人数．