题目内容
10.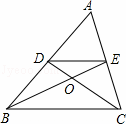 如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,则OC=( )
如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,若OD=2,则OC=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据重心定义得到点O为△ABC的重心,再根据重心的性质得$\frac{OC}{OD}$=2,所以OC=4.
解答 解:∵点D、E分别为AB、AC的中点,
∴点O为△ABC的重心,
∴$\frac{OC}{OD}$=2,
而OD=2,
∴OC=2OD=4.
故选B.
点评 本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
18.下列分解因式正确的是( )
| A. | m2+n2=(m+n)2 | B. | 16m2-4n2=(4m-n)(4m+2n) | ||
| C. | a3-3a2+a=a(a2-3a) | D. | 4a2-4ab+b2=(2a-b)2 |
5.正八边形的中心角是( )
| A. | 45° | B. | 135° | C. | 360° | D. | 1080° |
15.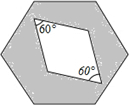 如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,边长为a的正六边形,里面有一菱形,边长也为a,空白部分面积为S1,阴影部分面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{9}$ |
20.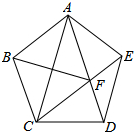 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
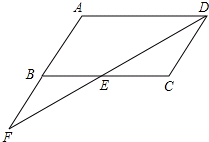 已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.
已知:如图,在平行四边形ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.若EC=3,求AD的长.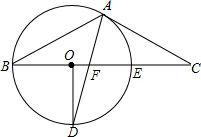 如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.
如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.