题目内容
7.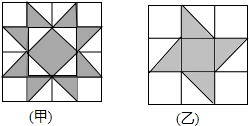 如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )| A. | P1<P2 | B. | P1=P2 | C. | P1>P2 | D. | 无法确定 |
分析 先根据甲和乙给出的图形,先求出黑色方砖在整个地板中所占的比值,再根据其比值即可得出结论.
解答 解:由图甲可知,黑色方砖6块,共有16块方砖,
∴黑色方砖在整个地板中所占的比值=$\frac{6}{16}$=$\frac{3}{8}$,
∴在乙种地板上最终停留在黑色区域的概率为P1是$\frac{3}{8}$,
由图乙可知,黑色方砖3块,共有9块方砖,
∴黑色方砖在整个地板中所占的比值=$\frac{3}{9}$=$\frac{1}{3}$,
∴在乙种地板上最终停留在黑色区域的概率为P2是$\frac{1}{3}$,
∵$\frac{3}{8}$>$\frac{1}{3}$,
∴P1>P2;
故选C.
点评 本题考查的是几何概率,用到的知识点为:几何概率=相应的面积与总面积之比.

练习册系列答案
相关题目
19.小德从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60米,下坡路每分钟走80米,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?若设小德从家里到学校的平路是x米,下坡路y米,根据题意列方程组为( )
| A. | $\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=15}\\{\frac{y}{40}+\frac{x}{60}=10}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=10}\\{\frac{y}{80}+\frac{x}{40}=15}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{60}+\frac{y}{80}=10}\\{\frac{y}{40}+\frac{x}{60}=15}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{40}+\frac{y}{80}=10}\\{\frac{y}{40}+\frac{x}{60}=15}\end{array}\right.$ |
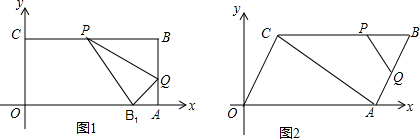
 如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.