题目内容
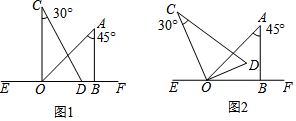
5.已知x为任意实数,则$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-8x+17}$的最小值为2$\sqrt{13}$.分析 因为$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-8x+17}$=$\sqrt{{x}^{2}+{5}^{2}}$+$\sqrt{(x-4)^{2}+{1}^{2}}$,所以欲求$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-8x+17}$的最小值,相当于如图A(0,5),B(4,1),在x轴上找一点P,使得PA+PB最短,作点B关于x轴的对称点B′(4,-1),PA+PB的最小值为AB′的长.
解答 解:∵$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-8x+17}$=$\sqrt{{x}^{2}+{5}^{2}}$+$\sqrt{(x-4)^{2}+{1}^{2}}$,
∴欲求$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-8x+17}$的最小值,相当于如图A(0,5),B(4,1),在x轴上找一点P,使得PA+PB最短, 作点B关于x轴的对称点B′(4,-1),
作点B关于x轴的对称点B′(4,-1),
PA+PB的最小值为AB′的长=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
∴$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-8x+17}$的最小值为2$\sqrt{13}$.
故答案为2$\sqrt{13}$.
点评 本题考查轴对称-最短问题、二次根式等知识,解题的关键是学会用转化的思想思考问题,把代数问题转化为几何问题解决,属于中考填空题中的压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.$\frac{2}{3}$的相反数是( )
| A. | $\frac{3}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{2}{3}$ |
15.9的算术平方根是( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 9 | D. | ±3 |

 解不等式(组),并把第(2)的解集表示在数轴上.
解不等式(组),并把第(2)的解集表示在数轴上.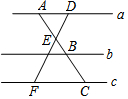 如图,直线a∥b∥c,若$\frac{AB}{BC}$=$\frac{4}{3}$,则$\frac{DE}{DF}$=$\frac{4}{7}$.
如图,直线a∥b∥c,若$\frac{AB}{BC}$=$\frac{4}{3}$,则$\frac{DE}{DF}$=$\frac{4}{7}$.