题目内容
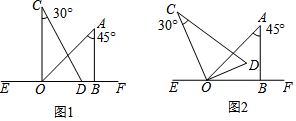
17.如图,将一幅三角板按照如图1所示的位置放置在直线EF上,现将含30°角的三角板OCD绕点O逆时针旋转180°,在这个过程中.(1)如图2,当OD平分∠AOB时,试问OC是否也平分∠AOE,请说明理由.
(2)当OC所在的直线平分∠AOE时,求∠AOD的度数;
(3)试探究∠BOC与∠AOD之间满足怎样的数量关系,并说明理由.
分析 (1)根据角平分线的定义,平角的定义即可求解;
(2)根据角平分线的定义和平角的定义求得∠AOC的度数,再根据角的和差关系即可求解;
(3)根据角的和差关系即可求解.
解答 解:(1)当OD平分∠AOB时,OC也平分∠AOE,
∵OD平分∠AOB时,
∴∠AOD=∠DOB,
∵∠AOD+∠DOB=90°,
∴∠COE+∠DOB=90°,
∴∵∠AOD=∠COE,
∴OC也平分∠AOE;
(2)∵OC所在的直线平分∠AOE,
∴∠AOC=$\frac{1}{2}$×(180°-45°)=67.5°,
∴∠AOD=90°-67.5°=22.5°;
(3)当∠AOD在∠AOB内部时,
∠AOD+∠BOC
=∠AOD+∠BOD+∠COD
=∠AOB+∠COD
=45°+90°
=135°;
当∠AOD在∠AOB外部时,
∠BOC-∠AOD
=∠AOB+∠COD
=45°+90°
=135°.
点评 此题考查了角平分线的定义,角的计算,关键是观察图形得到角与角之间的关系.

练习册系列答案
相关题目
8.钟表上的时间为9时30分,则时针与分针的夹角度数为( )
| A. | 90° | B. | 105° | C. | 120° | D. | 150° |
 如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.
如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.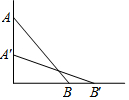 如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.
如图,一根长为a的竹竿AB斜靠在墙上,竹竿AB的倾斜角为α,当竹竿的顶端A下滑到点A'时,竹竿的另一端B向右滑到了点B',此时倾斜角为β.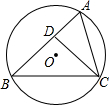 如图,△ABC是⊙O的内接三角形,CD⊥AB于D,若AD=3,BC=10,CD=6,则⊙O的半径为$\frac{5\sqrt{5}}{2}$.
如图,△ABC是⊙O的内接三角形,CD⊥AB于D,若AD=3,BC=10,CD=6,则⊙O的半径为$\frac{5\sqrt{5}}{2}$.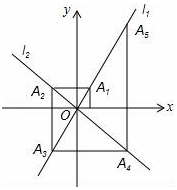 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2015的坐标为(-21007,-21008).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2015的坐标为(-21007,-21008).