题目内容
14.(1)计算:(-2)2-$\frac{\sqrt{3}}{2}$(1+tan45°)(2)先化简,再求值:$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}+\frac{b}{a+b}$,其中a=$\sqrt{2}$-2,b=$\sqrt{2}$+2.
分析 (1)先算平方,特殊角的三角函数值,再计算小括号里面的加法,再计算括号外面的乘法和减法;
(2)原式中两项通分并利用同分母分式的加法法则计算,再约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:(1)(-2)2-$\frac{\sqrt{3}}{2}$(1+tan45°)
=4-$\frac{\sqrt{3}}{2}$×(1+1)
=4-$\frac{\sqrt{3}}{2}$×2
=4-$\sqrt{3}$;
(2)$\frac{{a}^{2}-2ab+{b}^{2}}{{a}^{2}-{b}^{2}}+\frac{b}{a+b}$
=$\frac{(a-b)^{2}}{(a+b)(a-b)}$+$\frac{b}{a+b}$
=$\frac{a-b}{a+b}$+$\frac{b}{a+b}$
=$\frac{a}{a+b}$,
当a=$\sqrt{2}$-2,b=$\sqrt{2}$+2时,原式=$\frac{\sqrt{2}-2}{\sqrt{2}-2+\sqrt{2}+2}$=$\frac{1-\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
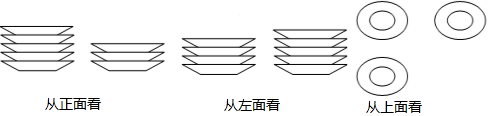
4.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
| 碟子的个数 | 1 | 2 | 3 | 4 | … |
| 碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
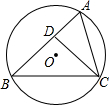 如图,△ABC是⊙O的内接三角形,CD⊥AB于D,若AD=3,BC=10,CD=6,则⊙O的半径为$\frac{5\sqrt{5}}{2}$.
如图,△ABC是⊙O的内接三角形,CD⊥AB于D,若AD=3,BC=10,CD=6,则⊙O的半径为$\frac{5\sqrt{5}}{2}$.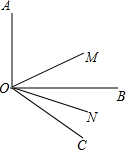 如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.
如图,OB是∠AOC内的一条射线,OM平分∠AOC,ON平分∠BOC,其中∠BOC是锐角.