题目内容
20．
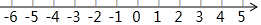解不等式（组），并把第（2）的解集表示在数轴上．（1）7x-2≥5x+2；
（2）$\left\{\begin{array}{l}4x-2＞3（{x-2}）\\ \frac{2x+1}{3}-\frac{1-x}{2}≤1\end{array}\right.$．
分析 （1）移项，合并同类项，系数化成1即可；
（2）先求出每个不等式的解集，再求出不等式组的解集，最后表示出来即可．
解答 解：（1）7x-2≥5x+2，
7x-5x≥2+2，
2x≥4，
x≥2；
（2）$\left\{\begin{array}{l}{4x-2＞3（x-2）①}\\{\frac{2x+1}{3}-\frac{1-x}{2}≤1②}\end{array}\right.$
∵解不等式①得：x＞-4，
解不等式②得：x≤1，
∴不等式组的解集为：-4＜x≤1，
在数轴上表示为：
．
点评 本题考查了解一元一次不等式组和解一元一次不等式，能根据不等式的解集找出不等式组的解集是解（2）的关键，能正确根据不等式的性质进行变形是解（1）的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知点A，B，C，D都在⊙O上，AC经过点O，且AC⊥BD，若∠ACB=50°，则∠ACD的度数为50°，∠BAD的度数为80°．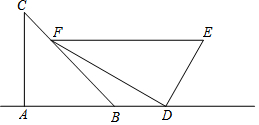
王生是一位善于思考的学生，在一次数学活动课上，他将一副直角三角板如图位置摆放，A、B、D在同一直线上，EF∥AD，∠A=∠EDF=90°，∠C=45°，∠E=60°，量得DE=4．求：
8．钟表上的时间为9时30分，则时针与分针的夹角度数为（ ）
| A． | 90° | B． | 105° | C． | 120° | D． | 150° |
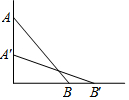如图，一根长为a的竹竿AB斜靠在墙上，竹竿AB的倾斜角为α，当竹竿的顶端A下滑到点A'时，竹竿的另一端B向右滑到了点B'，此时倾斜角为β．