题目内容
2.如图1,在某段公路上有一条双行线隧道(可双向行驶).隧道的纵截面由矩形的三边和一段抛物线构成,如图2是它的示意图,隧道宽度AB=8m,内壁两侧各留有1m宽的安全带,顶部最高处距路面6m,矩形的宽AD=2m.(1)为了保证安全,交通部门要求行驶车辆的顶部(设为平顶)与隧道的顶部在竖直方向上的高度差至少要0.5m,求一辆宽为3m的货运卡车通过该隧道时的限高应为多少?
(2)若有一辆宽为5.5m的超宽箱式工程车欲通过该隧道,其顶部与隧道顶部在竖直方向上的高度差不小于10cm,在实行交通管制后,求这辆车单向通过该隧道的限高应为多少?(结果精确到1m)
分析 (1)建立坐标系得出求出抛物线解析式,再求出x=3时y的值,结合竖直方向上的高度差至少要0.5m可得答案;
(2)根据以上解析式求得x=$\frac{11}{4}$时y的值,由竖直方向上的高度差不小于10cm可得答案.
解答 解:(1)以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,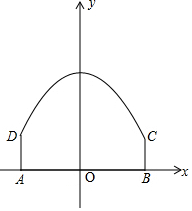
根据题意可知点C(4,2),抛物线的顶点坐标为(0,6),
设抛物线解析式为y=ax2+6,
将点C(4,2)代入,得:16a+6=2,
解得:a=-$\frac{1}{4}$,
则抛物线解析式为y=-$\frac{1}{4}$x2+6,
当x=3时,y=-$\frac{1}{4}$×32+6=$\frac{15}{4}$,
$\frac{15}{4}$-$\frac{1}{2}$=$\frac{13}{4}$=3.25(米),
答:宽为3m的货运卡车通过该隧道时的限高应为3.25m;
(2)由题意,当x=$\frac{11}{4}$时,y=-$\frac{1}{4}$×($\frac{11}{4}$)2+6=$\frac{263}{64}$,
$\frac{263}{64}$-0.1≈4(米),
答:这辆车单向通过该隧道的限高应为4米.
点评 本题主要考查二次函数的应用,建立合适坐标系求得抛物线解析式是前提和根本,理解题意计算相关数量是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.安徽省作为首批国家电子商务进农村示范省之一,先后携手阿里巴巴、苏宁云商等电商巨头,推动线上线下融合发展,激发农村消费潜力,实现“安徽特产卖全国”.根据某淘宝农村超市统计一月份的营业额为36万元,三月份的营业额为49万元.设每月的平均增长率为x,则可列方程为( )
| A. | 49(1+x)2=36 | B. | 36(1-x)2=49 | C. | 36(1+x)2=49 | D. | 49(1-x)2=36 |
10.互联网信息丰富了人类生活的新空间.据统计,目前我国约有670 000 000网民,将670 000 000用科学记数法表示为( )
| A. | 6.7×109 | B. | 6.7×108 | C. | 6.7×107 | D. | 0.67×108 |
7.全国31个省(市、自治区)的年度经济数据已全部公布,某省以37010亿元的经济总量仍在全国排名中位居第五,同比增长8.3%,高于全国1.4个百分点,把数据37010亿元用科学记数法表示为( )
| A. | 0.37010×1013元 | B. | 3.7010×1012元 | C. | 3.7010×1011元 | D. | 37010×1013元 |
14.下列条件中,不能判定四边形ABCD是平行四边形的是( )
| A. | AD∥BC,∠A=∠C | B. | ∠A=∠C,∠B=∠D | ||
| C. | AB∥CD,AB=DC | D. | AB∥CD,∠A+∠C=180° |
 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.
如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.