题目内容
14.下列条件中,不能判定四边形ABCD是平行四边形的是( )| A. | AD∥BC,∠A=∠C | B. | ∠A=∠C,∠B=∠D | ||
| C. | AB∥CD,AB=DC | D. | AB∥CD,∠A+∠C=180° |
分析 根据平行四边形的判断定理分别作出判断得出即可.
解答 解:A、由AD∥BC,∠A=∠C,可知∠A+∠B=180°,所以∠B+∠C=180°,所以AB∥CD,故能判断这个四边形是平行四边形,不合题意;
B、根据平行四边形的判定定理:两组对角分别相等的四边形是平行四边形,故能判断这个四边形是平行四边形,不合题意;
C、根据平行四边形的判定定理:一组对边分别相等且平行的四边形是平行四边形,不合题意;
D、由AB∥CD,∠A+∠C=180°,可以证明四边形ABCD是等腰梯形,不是平行四边形,符合题意.
故选:D.
点评 题主要考查了平行四边形的判定定理,准确无误的掌握定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.8的平方根是( )
| A. | 2 | B. | ±2 | C. | 2$\sqrt{2}$ | D. | $±2\sqrt{2}$ |
6. 如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )
如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )
 如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )
如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )| A. | 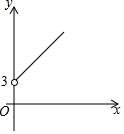 | B. | 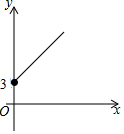 | C. | 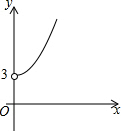 | D. | 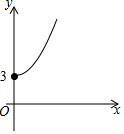 |
3.下列命题为真命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | b边形的外角和为(n-2)=180° | |
| D. | 若$\overline{{x}_{乙}}$=$\overline{{x}_{甲}}$,S${\;}_{甲}^{2}$>S${\;}_{乙}^{2}$,则甲数据更稳定 |
4.若二次函数y=ax2+bx-4的图象开口向上,与x轴的交点为(4,0)、(-2,0),则当x1=-1,x2=2时,对应的函数值y1和y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
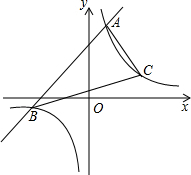 如图,已知一次函数y1=x+b(b>0)的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.
如图,已知一次函数y1=x+b(b>0)的图象与反比例函数y2=$\frac{6}{x}$的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.