题目内容
12．将6个小球分成两组，每组3个，第一组的小球的颜色分别是红、蓝、白，第二组的小球的颜色分别是红、黑、白，这6个小球除颜色不同外，其余均相同，将这两组小球分别放入两个不透明的袋子中搅匀，再从每个袋子中各随机摸出1个小球，请用画树状图或列表法求摸出的2个小球颜色相同的概率．分析 画树状图展示所有9种等可能的结果数，再找出摸出的2个小球颜色相同的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有9种等可能的结果数，其中摸出的2个小球颜色相同的结果数为2，
所以摸出的2个小球颜色相同的概率=$\frac{2}{9}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．．
练习册系列答案
阅读快车系列答案
相关题目
3．下列命题为真命题的是（ ）
| A． | 若a2=b2，则a=b | |
| B． | 等角的补角相等 | |
| C． | b边形的外角和为（n-2）=180° | |
| D． | 若$\overline{{x}_{乙}}$=$\overline{{x}_{甲}}$，S${\;}_{甲}^{2}$＞S${\;}_{乙}^{2}$，则甲数据更稳定 |
20．
在四边形ABCD中，如果∠A+∠B+∠C=260°，那么∠D的度数为（ ）
在四边形ABCD中，如果∠A+∠B+∠C=260°，那么∠D的度数为（ ）| A． | 120° | B． | 110° | C． | 100° | D． | 90° |
7．
如图，在矩形ABCD中，AB=4，AD=5，AD、AB、BC分别与⊙O相切于E、F、G三点，过点D作⊙O的切线交BC于点M，切点为N，则DM的长为（ ）
如图，在矩形ABCD中，AB=4，AD=5，AD、AB、BC分别与⊙O相切于E、F、G三点，过点D作⊙O的切线交BC于点M，切点为N，则DM的长为（ ）| A． | $\frac{9}{2}$ | B． | 2$\sqrt{5}$ | C． | $\frac{4\sqrt{13}}{3}$ | D． | $\frac{13}{3}$ |
17．
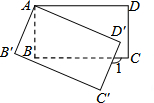如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，若旋转角为20°，则∠1为（ ）
如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，若旋转角为20°，则∠1为（ ）| A． | 110° | B． | 120° | C． | 150° | D． | 160° |
4．若二次函数y=ax2+bx-4的图象开口向上，与x轴的交点为（4，0）、（-2，0），则当x1=-1，x2=2时，对应的函数值y1和y2的大小关系为（ ）
| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 不确定 |
1．下列运算正确的是（ ）
| A． | 3a+2a=5a2 | B． | 3-3=$\frac{1}{27}$ | C． | 2a2•a2=2a6 | D． | 60=0 |
2．今年我市有近5万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说法正确的是（ ）
| A． | 这1000名考生是总体的一个样本 | B． | 近5万名考生是总体 | ||
| C． | 每位考生的数学成绩是个体 | D． | 1000名学生的数学成绩是样本容量 |