题目内容
11. 如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.
如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=$\frac{1}{2}$,直线l上的点P位于y轴左侧,且到y轴的距离为1.(1)求直线l的解析式;
(2)若反比例函数y=$\frac{m}{x}$的图象经过点P,求m的值及反比例函数的解析式;
(3)若一抛物线过A,P两点,且对称轴为y轴,求此抛物线的顶点坐标.
分析 (1)由OA=2、tan∠OAB=$\frac{OB}{OA}$=$\frac{1}{2}$可得点B坐标(0,1),利用待定系数法求解可得直线l解析式;
(2)由题意得出点P的横坐标为-1,将x=-1代入直线l解析式求得点P坐标,待定系数法求解可得;
(3)根据A、P两点待定系数法求解可得.
解答 解:(1)∵点A(2,0),即OA=2,且tan∠OAB=$\frac{OB}{OA}$=$\frac{1}{2}$,
∴OB=1,即点B(0,1),
设直线l的解析式为y=kx+b,
将点A(2,0)、B(0,1)代入,得:$\left\{\begin{array}{l}{2k+b=0}\\{b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
则直线l的解析式为y=-$\frac{1}{2}$x+1;
(2)∵点P到y轴的距离为1,且点P位于y轴左侧,
∴点P的横坐标为-1,
则当x=-1时,y=-$\frac{1}{2}$×(-1)+1=$\frac{3}{2}$,
∴点P的坐标为(-1,$\frac{3}{2}$),
代入y=$\frac{m}{x}$得:$\frac{3}{2}$=$\frac{m}{-1}$,即m=-$\frac{3}{2}$,
则反比例函数解析式为y=-$\frac{\frac{3}{2}}{x}$=-$\frac{3}{2x}$;
(3)设抛物线解析式为y=ax2+c,
将点P(-1,$\frac{3}{2}$)、A(2,0)代入,得:$\left\{\begin{array}{l}{a+c=\frac{3}{2}}\\{4a+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$,
则抛物线的解析式为y=-$\frac{1}{2}$x+2,其顶点坐标为(0,2).
点评 本题主要考查待定系数法求函数解析式和解直角三角形,熟练掌握待定系数求函数解析式是解题的关键.

 如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )
如图,点A的坐标为(0,3),点B是x轴正半轴上的一个动点,以AB为边作等腰直角△ABC,使∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象的是( )| A. | 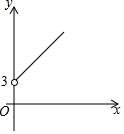 | B. | 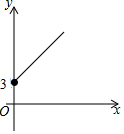 | C. | 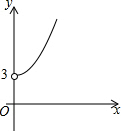 | D. | 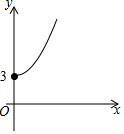 |
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | b边形的外角和为(n-2)=180° | |
| D. | 若$\overline{{x}_{乙}}$=$\overline{{x}_{甲}}$,S${\;}_{甲}^{2}$>S${\;}_{乙}^{2}$,则甲数据更稳定 |
 在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )
在四边形ABCD中,如果∠A+∠B+∠C=260°,那么∠D的度数为( )| A. | 120° | B. | 110° | C. | 100° | D. | 90° |
| A. | 3a+2a=5a2 | B. | 3-3=$\frac{1}{27}$ | C. | 2a2•a2=2a6 | D. | 60=0 |