题目内容
 全面实现低碳生活已逐渐成为人们的共识.某企业为了发展低碳经济,采用技术革新,减少二氧化碳的排放.随着排放量的减少,企业相应获得的利润也有所提高,且相应获得的利润y(万元)与月份x(月)
全面实现低碳生活已逐渐成为人们的共识.某企业为了发展低碳经济,采用技术革新,减少二氧化碳的排放.随着排放量的减少,企业相应获得的利润也有所提高,且相应获得的利润y(万元)与月份x(月)(1≤x≤6)的函数关系如图所示:
(1)根据图象,请判断:y与x(1≤x≤6)的变化规律应该符合
(填写序号:①反比例函数、②一次函数、③二次函数);
(2)求出y与x(1≤x≤6)的函数关系式(不写取值范围);
(3)经统计发现,从6月到8月每月利润的增长率相同,且8月份的利润为151.2万元,求这个增长率.
考点:一次函数的应用,一元二次方程的应用
专题:
分析:(1)根据图象是一条直线,可得函数的类型;
(2)根据待定系数法,可得函数解析式;
(3)根据自变量的值,可得相应的函数值,根据等量关系,可得方程,根据解方程,可得答案.
(2)根据待定系数法,可得函数解析式;
(3)根据自变量的值,可得相应的函数值,根据等量关系,可得方程,根据解方程,可得答案.
解答:解:(1)②;
(2)设函数解析式为y=kx+b (a≠0),
将(1,80)、(4,95)代入得:
,
∴
∴一次函数的解析式是y=5x+75;
(3)把x=6代入y=5x+75
得y=105,
6月份的收入是105万元,
设这个增长率是a,根据题意得
105(1+a)2=151.2,
解得∴a1=
,a2=-
(不合题意,舍去)
答:这个增长率是20%.
(2)设函数解析式为y=kx+b (a≠0),
将(1,80)、(4,95)代入得:
|
∴
|
∴一次函数的解析式是y=5x+75;
(3)把x=6代入y=5x+75
得y=105,
6月份的收入是105万元,
设这个增长率是a,根据题意得
105(1+a)2=151.2,
解得∴a1=
| 1 |
| 5 |
| 11 |
| 5 |
答:这个增长率是20%.
点评:本题考查了一次函数的应用,利用待定系数法求解析式,(3)找出等量关系列方程是解题关键,不符合题意的要舍去.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
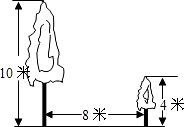 如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A、8米 | B、10米 |
| C、12米 | D、14米 |
 已知抛物线对应的二次函数为y=a(x+10)(x+5),它与x轴交于A、B两点(A在B的左侧),与y轴交于C点,点D是以B为圆心、5为半径的圆周上位于第二象限内的动点,直线AD与y轴交于点E,设E(0,2t).
已知抛物线对应的二次函数为y=a(x+10)(x+5),它与x轴交于A、B两点(A在B的左侧),与y轴交于C点,点D是以B为圆心、5为半径的圆周上位于第二象限内的动点,直线AD与y轴交于点E,设E(0,2t).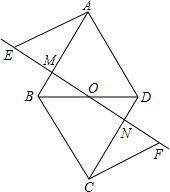 如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.
如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.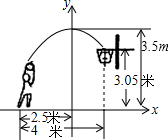 如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.
如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.