题目内容
在Rt△ABC中,∠C=90°,已知AC=6cm,BC=8cm.
(1)求AB边上中线CM的长;
(2)点P是线段CM上一动点(点P与点C、点M不重合),求出△APB的面积y(平方厘米)与CP的长x(厘米)之间的函数关系式并求出函数的定义域;
(3)是否存在这样的点P,使得△ABP的面积是凹四边形ACBP面积的
?如果存在,请求出CP的长;如果不存在,请说明理由.
(1)求AB边上中线CM的长;
(2)点P是线段CM上一动点(点P与点C、点M不重合),求出△APB的面积y(平方厘米)与CP的长x(厘米)之间的函数关系式并求出函数的定义域;
(3)是否存在这样的点P,使得△ABP的面积是凹四边形ACBP面积的
| 3 |
| 2 |
考点:勾股定理,三角形的面积,直角三角形斜边上的中线
专题:
分析:(1)在直角三角形中,已知两直角边,根据勾股定理即可求斜边的长,根据斜边的中线长是斜边长的一半的性质即可以解题;
(2)根据S△AMP=S△ACM-S△APC即可求出
y,从而可得出答案;
(3)△ABP的面积是凹四边形ACBP面积的
,可知△ABP的面积是△ACB面积的
,据此列出方程求解即可.
(2)根据S△AMP=S△ACM-S△APC即可求出
| 1 |
| 2 |
(3)△ABP的面积是凹四边形ACBP面积的
| 3 |
| 2 |
| 3 |
| 5 |
解答:解:(1)∵∠C=90°,AC=6cm,BC=8cm,
∴AB=
=5(cm),
在直角三角形中,根据斜边的中线长是斜边长的一半的性质,
∴CM=
AB=5(cm);
 (2)∵CP=x,CM=AM,
(2)∵CP=x,CM=AM,
∴∠CAB=∠ACM,
∵sin∠CAB=
=
,
∴sin∠ACM=
,
∴S△AMC=
×6×5×sin∠ACM=12(cm2),
S△ACP=
×6×x×
=
x(cm2),
∵△APB的面积y,
∴
y=S△AMC-S△ACP=12-
x,
∴y=24-
x(0<x<5);
(3)△ABP的面积是凹四边形ACBP面积的
时,
24-
x=
×6×8,
解得x=2.5.
故CP的长是2.5cm.
∴AB=
| 62+82 |
在直角三角形中,根据斜边的中线长是斜边长的一半的性质,
∴CM=
| 1 |
| 2 |
 (2)∵CP=x,CM=AM,
(2)∵CP=x,CM=AM,∴∠CAB=∠ACM,
∵sin∠CAB=
| BC |
| AB |
| 4 |
| 5 |
∴sin∠ACM=
| 4 |
| 5 |
∴S△AMC=
| 1 |
| 2 |
S△ACP=
| 1 |
| 2 |
| 4 |
| 5 |
| 12 |
| 5 |
∵△APB的面积y,
∴
| 1 |
| 2 |
| 12 |
| 5 |
∴y=24-
| 24 |
| 5 |
(3)△ABP的面积是凹四边形ACBP面积的
| 3 |
| 2 |
24-
| 24 |
| 5 |
| 1 |
| 2 |
解得x=2.5.
故CP的长是2.5cm.
点评:本题考查了一次函数及勾股定理,难度较大,关键是掌握在直角三角形中,斜边的中线长是斜边长的一半.

练习册系列答案
相关题目
一个多项式加上5x2-4x-3得x2-3x,则这个多项式为( )
| A、4x2-7x-3 |
| B、6x2-x-3 |
| C、-4x2+x+3 |
| D、-6x2-7x-3 |
把多项式2xn+2+4xn-6xn-2分解因式,其结果应是( )
| A、2xn(x2+2-3x)=2xn(x-1)(x-2) |
| B、2xn-2(x2-3x+2)=2xn-2(x-1)(x-2) |
| C、2xn-2(x4+2x2-3)=2xn-2(x2+3)(x2-1)=2xn-2(x2+3)(x+1)(x-1) |
| D、2xn-2(x4-2x2+3)=2xn-2 (x2+3)(x2+1) |

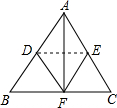 如图,沿DE折叠一张三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC.△DBF和△EFC是否为等腰三角形?请说明理由.
如图,沿DE折叠一张三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC.△DBF和△EFC是否为等腰三角形?请说明理由.