题目内容
如图,A,P,B,C是⊙O上的四个点,∠APC=∠BPC=60°,过点A作⊙O的切线交BP的延长线于点D.


(1)求证:△ADP∽△BD A;
A;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)若AD=2,PD=1,求线段BC的长.
(1)证明详见解析;(2) PA+PB=PC,证明详见解析;(3)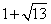
 .
.
【解析】
试题分析:(1)首先作⊙O的直径AE,连接PE,利用切线的性质以及圆周角定理得出∠PAD =∠PBA进而得出答案;
=∠PBA进而得出答案;
(2)首先在线段PC上截取PF=PB,连接BF,进而得出△BPA≌△BFC(AAS),即可得出PA+PB=PF+FC=PC;
(3)利用△ADP∽△BDA,得出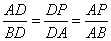
 ,求出BP的长,进而得出△ADP∽△CAP,则
,求出BP的长,进而得出△ADP∽△CAP,则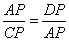
 ,则AP2=CP•PD求出AP的长,即可得出答案.
,则AP2=CP•PD求出AP的长,即可得出答案.

(3)解:∵△ADP∽△ BDA,∴
BDA,∴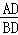
 =
=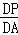
 =
=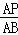
 ,
,
∵AD=2,PD=1∴BD=4,AB=2AP,∴BP=BD﹣DP=3,
∵∠APD=180°﹣∠BPA=60°,∴∠APD=∠APC,
∵∠PAD=∠E,∠PCA =∠E,∴PAD=∠PCA,∴△ADP∽△CAP,∴
=∠E,∴PAD=∠PCA,∴△ADP∽△CAP,∴
 =
=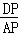
 ,
,
∴AP2=CP•PD,∴AP2=(3+AP)•1,
解得:AP=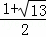
 或A
或A P=
P=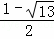
 (舍去),∴BC=AB=2AP=1+
(舍去),∴BC=AB=2AP=1+
 .
.


考点:切线 的性质;圆周角定理;全等三角形的判定和性质;相似三角形的判定和性质.
的性质;圆周角定理;全等三角形的判定和性质;相似三角形的判定和性质.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 的图象如下列四个图之一所示,根据
的图象如下列四个图之一所示,根据 图象分析,a的值等于【 】
图象分析,a的值等于【 】
 长方形ACBD和长方形AEFB(如图2)。
长方形ACBD和长方形AEFB(如图2)。

 中的要求把它补成长方形,那么符合要求的长方形可以画出 个,利用图3把它画出来。
中的要求把它补成长方形,那么符合要求的长方形可以画出 个,利用图3把它画出来。
 B.
B.  C.
C. 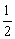 D.
D. 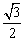
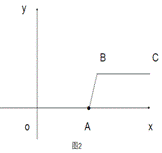
 =2时,如图1,线段BC与线段OA的距离是_____,
=2时,如图1,线段BC与线段OA的距离是_____,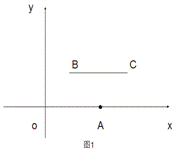


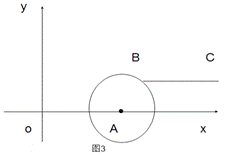





 到与AB相切于点D的位置,则⊙O自转了【 】
到与AB相切于点D的位置,则⊙O自转了【 】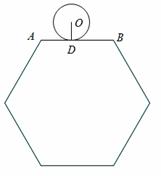
 BCD,其中AB=
BCD,其中AB= 2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
2,AD=1,将矩形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为