题目内容
5.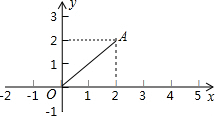 如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )
如图,点A的坐标为(2,2),若点P在坐标轴上,且△APO为等腰三角形,则满足条件的点P个数是( )| A. | 4个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 等腰三角形要判断腰长的情况,本题可根据OA是底边、腰几种情况着手进行讨论即可得出答案.
解答 解:已知点A的坐标为(2,2),则△OAP的边OA=2$\sqrt{2}$,这条边可能是底边也可能是腰.
①当OA是底边时,点P是OA的垂直平分线与坐标轴的交点,这两个点的坐标是(2,0)和(0,2);
②当OA是腰时,当O是顶角顶点时,以O为圆心,以OA为半径作圆,与坐标轴的交点坐标是(2$\sqrt{2}$,0),(-2$\sqrt{2}$,0),(0,2$\sqrt{2}$),(0,-2$\sqrt{2}$);
③当A是顶角顶点时,以A为圆心,以AO为半径作圆,与坐标轴的交点坐标是(4,0),(0,4).
故满足条件的点P共有8个.
故选D.
点评 本题考查了等腰三角形的判定、坐标与图形性质;分情况进行讨论,能够把各种情况能够讨论全是解决本题的关键.

练习册系列答案
相关题目
20.下列各点中,在第三象限的是( )
| A. | (2,3) | B. | (2,-1) | C. | (-2,6) | D. | (-1,-5) |
10.现有背面完全相同的四张扑克牌,牌面数字分别是2,3,4,5,洗匀后背面朝上,则从中任意翻开一张是2的倍数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
14.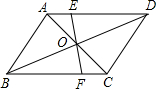 如图,四边形ABCD中,AB∥CD,AD∥BC,AC与BD相交于点O,过点O的直线EF交AB于点E,交CD于点F,则下列说法不正确的是( )
如图,四边形ABCD中,AB∥CD,AD∥BC,AC与BD相交于点O,过点O的直线EF交AB于点E,交CD于点F,则下列说法不正确的是( )
 如图,四边形ABCD中,AB∥CD,AD∥BC,AC与BD相交于点O,过点O的直线EF交AB于点E,交CD于点F,则下列说法不正确的是( )
如图,四边形ABCD中,AB∥CD,AD∥BC,AC与BD相交于点O,过点O的直线EF交AB于点E,交CD于点F,则下列说法不正确的是( )| A. | △ADC≌△CBA | B. | △AOB≌△COD | C. | DO=DF | D. | OE=OF |
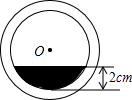 将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.
将一盛有不足半杯水的圆柱形玻璃水拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是($\frac{16}{3}$π-4$\sqrt{3}$)cm2.