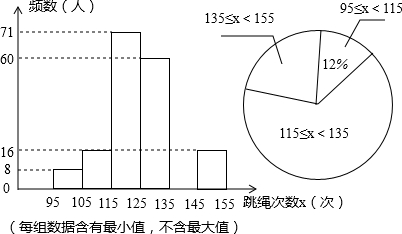
题目内容
13. 如图,一次函数y=$\frac{1}{2}$x-2与反比例函数y=$\frac{m}{x}$的图象交于点A,且点A的纵坐标为1.
如图,一次函数y=$\frac{1}{2}$x-2与反比例函数y=$\frac{m}{x}$的图象交于点A,且点A的纵坐标为1.(1)反比例函数的解析式;
(2)根据图象直接写出当x>0时,一次函数的值小于反比例函数的值的x的取值范围.
分析 (1)一次函数是完整的函数,把点A的纵坐标代入即可求得M的坐标;然后把A的坐标代入反比例函数解析式,即可求得反比例函数的解析式;
(2)根据交点A的坐标,即可得到当x>0时,一次函数的值大于反比例函数的值的x的取值范围.
解答 解:(1)点A在y=$\frac{1}{2}$x-2上,
∴1=$\frac{1}{2}$x-2,
解得x=6,
把(6,1)代入y=$\frac{m}{x}$得
m=6×1=6.
∴y=$\frac{6}{x}$;
(2)由图象得,当x>6时,一次函数的值大于反比例函数的值.
点评 本题考查用待定系数法求函数解析式;注意:无论是求自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;同时要注意反比例函数的自变量不能取0.

练习册系列答案
相关题目
3.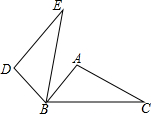 如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
 如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=40°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )| A. | 50° | B. | 70° | C. | 80° | D. | 90° |
8.下列命题中,是假命题的是( )
| A. | 成轴对称的两个图形是全等图形 | |
| B. | 直角三角形斜边上的中线等于斜边的一半 | |
| C. | 若x>y,则x-3>y-3 | |
| D. | ∠A的相邻外角是70°,要使△ABC为等腰三角形,则∠B为35°或110° |
5.某校初三学生开展毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每踢100个(含100)为优秀.下表是成绩最好的甲班和乙班各5名学生的比赛数据(单位:个)
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)计算两班的优秀率及比赛数据的中位数;
(2)哪一个班级学生的比赛成绩相互之间更接近,为什么?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?说明理由!
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率及比赛数据的中位数;
(2)哪一个班级学生的比赛成绩相互之间更接近,为什么?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?说明理由!
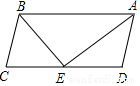 如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的是⑤
如图,在四边形ABCD中,AD∥BC,若∠DAB的角平分线AE交CD于E,连结BE,且BE边平分∠ABC,则以下命题不正确的是⑤