题目内容
18．解方程：$\frac{1}{x-4}$-$\frac{2}{x-3}$=$\frac{3}{x-2}$-$\frac{4}{x-1}$．分析 分式方程整理后，去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：方程整理得：$\frac{1}{x-4}$+$\frac{4}{x-1}$=$\frac{3}{x-2}$+$\frac{2}{x-3}$，即$\frac{5x-17}{（x-4）（x-1）}$=$\frac{5x-17}{（x-2）（x-3）}$，
当5x-17=0，即x=$\frac{17}{5}$时，方程成立；
当5x-17≠0时，化简得：x2-5x+4=x2-5x+6，无解，
经检验x=$\frac{17}{5}$是原分式方程的解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
教材全解字词句篇系列答案
相关题目
8．
为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了一部分学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：
学生最喜爱的节目人数统计表
根据以上提供的信息，解答下列问题：
（1）a=20，b=30；
（2）补全上面的条形统计图；
（3）若该校共有学生1600名，根据抽样调查结果，估计该校最喜爱《朗读者》节目的学生有多少名．
为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了一部分学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：学生最喜爱的节目人数统计表
| 节目 | 人数（名） | 百分比 |
| 最强大脑 | 5 | 10% |
| 朗读者 | 15 | b% |
| 中国诗词大会 | a | 40% |
| 出彩中国人 | 10 | 20% |
（1）a=20，b=30；
（2）补全上面的条形统计图；
（3）若该校共有学生1600名，根据抽样调查结果，估计该校最喜爱《朗读者》节目的学生有多少名．
9．下列各式计算正确的是（ ）
| A． | m3+m3=m6 | B． | m3•m3=2m3 | C． | 20160÷m-1=m | D． | （-m2）•（-m）2÷m=m3 |
6．
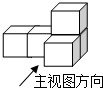如图是由五个相同的小正方体组成的几何体，则下列说法正确的是（ ）
如图是由五个相同的小正方体组成的几何体，则下列说法正确的是（ ）| A． | 左视图面积最大 | B． | 俯视图面积最小 | ||
| C． | 左视图面积和主视图面积相等 | D． | 俯视图面积和主视图面积相等 |
如图，一次函数y=$\frac{1}{2}$x-2与反比例函数y=$\frac{m}{x}$的图象交于点A，且点A的纵坐标为1．
10．满足不等式$\frac{x-3}{2}$＜1的非负整数解有（ ）
| A． | 0，1，2，3，4，5 | B． | 0，1，2，3，4 | C． | 1，2，3，4，5 | D． | 1，2，3，4 |
