题目内容
18.一个三角形三边分别是6,8,10,则这个三角形最长边上的高是( )| A. | 8 | B. | $\frac{20}{3}$ | C. | 5 | D. | $\frac{24}{5}$ |
分析 根据勾股定理逆定理先判定其形状,再根据直角三角形的面积公式求得其高.
解答 解:∵三角形的三边长分别为6,8,10,符合勾股定理的逆定理62+82=102,
∴此三角形为直角三角形,则10为直角三角形的斜边,
设三角形最长边上的高是h,
根据三角形的面积公式得:$\frac{1}{2}$×6×8=$\frac{1}{2}$×10h,
解得h=$\frac{24}{5}$.
故选:D.
点评 此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | (2x-3)2=4x2+12x-9 | B. | (4x+1)2=16x2+8x+1 | C. | (a+b)(a-b)=a2+b2 | D. | (2m+3)(2m-3)=4m2-3 |
 一个表面涂满色的正方体.
一个表面涂满色的正方体.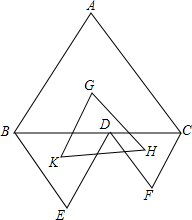 如图,在正△ABC底边BC上任取一点D,以BD、CD为边分别向外作正△BDE,正△CDF,设三个正三角形的中心分别为G、K、H,求证:△GKH也为正三角形.
如图,在正△ABC底边BC上任取一点D,以BD、CD为边分别向外作正△BDE,正△CDF,设三个正三角形的中心分别为G、K、H,求证:△GKH也为正三角形.