题目内容
10.方程3x2-x-1=0的两根是x1,x2,求下列式子的值:(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$;
(2)x12+x22.
分析 由于方程3x2-x-1=0的两个实数根为x1,x2,所以直接利用根与系数的关系即可得到两根之和和两根之积,然后代入化简后的代数式即可得到结果.
解答 解:∵方程3x2-x-1=0的两根是x1,x2,
∴x1+x2=$\frac{1}{3}$,x1•x2=-$\frac{1}{3}$,
(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{\frac{1}{3}}{-\frac{1}{3}}$=-1;
(2)x12+x22=(x1+x2)2-2x1x2=($\frac{1}{3}$)2-2×(-$\frac{1}{3}$)=$\frac{7}{9}$.
点评 本题考查了一元二次方程根与系数的关系,完全平方公式,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
18.一个三角形三边分别是6,8,10,则这个三角形最长边上的高是( )
| A. | 8 | B. | $\frac{20}{3}$ | C. | 5 | D. | $\frac{24}{5}$ |
2.若t是一元二次方程ax2+bx+c=0的根,记△=b2-4ac,则△和完全平方式$M={(at+\frac{b}{2})^2}$的关系是( )
| A. | △=M | B. | △=2M | C. | △=4M | D. | △=$\frac{1}{2}$M |
19.下列计算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | 5$\sqrt{3}$×5$\sqrt{2}$=5$\sqrt{6}$ | C. | $\sqrt{8}$÷$\sqrt{2}$=2 | D. | $\sqrt{(-6)^{2}}$=-6 |
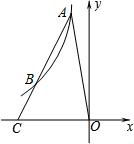 如图,点A、B在双曲线y=$\frac{k}{x}$上,AB的延长线交x轴于C,连OA.若AB=2BC,S△OAC=12,则k=-6.
如图,点A、B在双曲线y=$\frac{k}{x}$上,AB的延长线交x轴于C,连OA.若AB=2BC,S△OAC=12,则k=-6. 已知:在等腰Rt△ABC中,AC=BC,∠C=90°,AD平分∠BAC,DE⊥AB于点E.求证:BD+DE=AC.
已知:在等腰Rt△ABC中,AC=BC,∠C=90°,AD平分∠BAC,DE⊥AB于点E.求证:BD+DE=AC.