题目内容
19.问题引入:(1)如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=90°+$\frac{1}{2}$α(用α表示);如图②,∠CBO=$\frac{1}{3}$∠ABC,∠BCO=$\frac{1}{3}$∠ACB,∠A=α,则∠BOC=120°+$\frac{1}{3}$α(用α表示)
拓展研究:
(2)如图③,∠CBO=$\frac{1}{3}$∠DBC,∠BCO=$\frac{1}{3}$∠ECB,∠A=α,请猜想∠BOC=120°-$\frac{1}{3}$α(用α表示),并说明理由.
类比研究:
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=$\frac{1}{n}$∠DBC,∠BCO=$\frac{1}{n}$∠ECB,∠A=α,请猜想∠BOC=$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
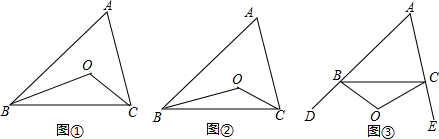
分析 (1)如图①,根据角平分线的定义可得∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,然后表示出∠OBC+∠OCB,再根据三角形的内角和等于180°列式整理即可得∠BOC=90°+$\frac{1}{2}$α;如图②,根据三角形的内角和等于180°列式整理即可得∠BOC=120°+$\frac{1}{3}$α;
(2)如图③,根据三角形的内角和等于180°列式整理即可得∠BOC=120°-$\frac{1}{3}$α;
(3)根据三角形的内角和等于180°列式整理即可得∠BOC=$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
解答 解:(1)如图①,∵∠ABC与∠ACB的平分线相交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A
=90°+$\frac{1}{2}$α; 如图②,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
如图②,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{3}$(∠ABC+∠ACB)
=180°-$\frac{1}{3}$(180°-∠A)
=120°+$\frac{1}{3}$∠A
=120°+$\frac{1}{3}$α;
(2)如图③,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{3}$(∠DBC+∠ECB)
=180°-$\frac{1}{3}$(∠A+∠ACB+∠A+ABC)
=180°-$\frac{1}{3}$(∠A+180°)
=120°-$\frac{1}{3}$α;
(3)在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{n}$(∠DBC+∠ECB)
=180°-$\frac{1}{n}$(∠A+∠ACB+∠A+ABC)
=180°-$\frac{1}{n}$(∠A+180°)
=$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
故答案为90°+$\frac{1}{2}$α,120°+$\frac{1}{3}$α;120°-$\frac{1}{3}$α;$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
点评 本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

| A. | a>0,m>0 | B. | a>0,n<0 | C. | m>0,n<0 | D. | m<0,n<0 |
| A. | a3•a2 | B. | a10÷a2 | C. | (a2)3 | D. | (-a)5 |
| A. | 8x6÷2x3=4x2 | B. | x2+x3=x5 | C. | (-3x2y)3=-9x6y3 | D. | x•x2=x3 |
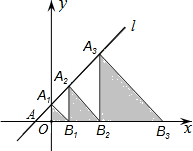 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn顶点Bn的横坐标为2n+1-2.
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn顶点Bn的横坐标为2n+1-2. 如图,已知∠CAB=∠DBA,∠CBD=∠DAC.
如图,已知∠CAB=∠DBA,∠CBD=∠DAC.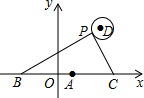 如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是6.
如图,在平面直角坐标系中,已知点A(1,0),B(1-a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是6.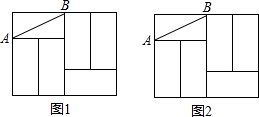 如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.