题目内容
9.要使二次函数y=a(x+m)2+n(a≠0)的图象与x轴有两个交点,下列条件中正确的是( )| A. | a>0,m>0 | B. | a>0,n<0 | C. | m>0,n<0 | D. | m<0,n<0 |
分析 根据二次函数图象与x轴有两个交点,则方程a(x+m)2+n=0有两个不相等的实数根,得-$\frac{n}{a}$>0,说明a、n异号,即当a>0时n<0;或当a<0时n>0.
解答 解:当y=0时,a(x+m)2+n=0,
a(x+m)2=-n,
(x+m)2=-$\frac{n}{a}$,
要使二次函数y=a(x+m)2+n(a≠0)的图象与x轴有两个交点,则-$\frac{n}{a}$>0,
$\frac{n}{a}$<0,则a、n异号.
故选:B.
点评 本题考查了抛物线与x轴的交点,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标;若判断抛物线与x轴的交点的个数,计算△=b2-4ac决定抛物线与x轴的交点个数;如果不是一般式,对于二次函数y=a(x-h)2+k,利用a与k的符号来判断抛物线与x轴的交点个数.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.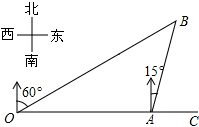 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )| A. | 4km | B. | 2$\sqrt{3}$km | C. | 2$\sqrt{2}$km | D. | ($\sqrt{3}$+1)km |
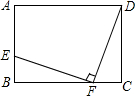 已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.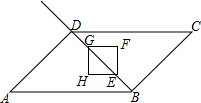 如图,在平行四边形ABCD中,AB=4$\sqrt{2}$,∠A=45°,∠ADB=90°,点E从点B出发,以每秒1个单位的速度向终点D运动.点G在射线BD上,且EG=2BE(点G在E上方),以EG为对角线作正方形EFGH,设点E的运动时间为t(秒).
如图,在平行四边形ABCD中,AB=4$\sqrt{2}$,∠A=45°,∠ADB=90°,点E从点B出发,以每秒1个单位的速度向终点D运动.点G在射线BD上,且EG=2BE(点G在E上方),以EG为对角线作正方形EFGH,设点E的运动时间为t(秒).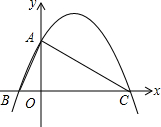 已知,如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
已知,如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.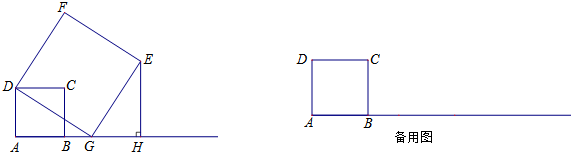
 如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.