题目内容
3．
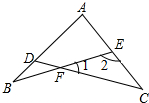如图，∠B=25°，∠C=35°，∠A-∠1=60°，求∠A的度数．
分析 设∠A=x，则∠2=∠A+∠B=x+25°，由三角形内角和定理得出∠1+x=120°，再由已知条件得出x=90°即可．
解答 解：设∠A=x，则∠2=∠A+∠B=x+25°，
在△CEF中，∠1+∠2+∠C=180°，
∴∠1+∠2+35°=180°，
∴∠1+x+25°=145°，
∴∠1+x=120°①，
又∵x-∠1=60°②，
∴①+②得：2x=180°，
∴x=90°，
即∠A=90°．
点评 本题考查了三角形内角和定理、三角形的外角性质；熟练掌握三角形内角和定理，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
14．（-$\frac{2}{3}$）2015×（$\frac{3}{2}$）2014等于（ ）
| A． | 1 | B． | -$\frac{2}{3}$ | C． | -1 | D． | $\frac{2}{3}$ |
如图，某小区内有一块长、宽比为2：1的矩形空地，计划在该空地上修筑两条宽为2m的互相垂直的小路，余下的四块小矩形空地铺成草坪，如果四块草坪的面积之和为312m2，请求出原来大矩形空地的长和宽．