题目内容
6.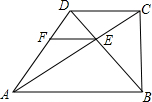 如图,直角梯形ABCD中,AB∥DC,∠ABC﹦90°,AD﹦BD,AC与BD相交于点E,AC⊥BD,过点E作EF∥AB交AD于F.
如图,直角梯形ABCD中,AB∥DC,∠ABC﹦90°,AD﹦BD,AC与BD相交于点E,AC⊥BD,过点E作EF∥AB交AD于F.(1)说明AF﹦BE的理由;
(2)AF2与AE•EC有怎样的数量关系?为什么?
分析 (1)根据平行构造相似三角形,利用相似三角形的性质解答;
(2)因为AB⊥BC,所以△ABC为直角三角形,又因为AC⊥BD,所以可知△BCE∽△ABE,利用相似三角形的性质即可解答.
解答 证明:(1)∵EF∥AB,
∴△DFE∽△DAB.
∴$\frac{DF}{DA}$=$\frac{DE}{DB}$,
又∵DA=DB,
∴DF=DE.
∴DA-DF=DB-DE,即AF=BE.
(2)AF2=AE•EC.
∵AB⊥BC,
∴△ABC为直角三角形.
又∵AC⊥BD,
∴△BCE∽△ABE.
∴$\frac{EB}{EC}$=$\frac{AE}{EB}$,即EB2=AE•EC.
又∵AF=EB,
∴AF2=AE•EC.
点评 本题考查了相似三角形的判定和性质,解答此题的关键是根据平行和直角三角形的性质找出图中的相似三角形,利用相似三角形的性质解答此题.

练习册系列答案
相关题目
18.过点A(-3,3)和点B(6,3)的直线一定( )
| A. | 垂直于x轴 | B. | 于y轴相交但不平行于x轴 | ||
| C. | 平行于x轴 | D. | 平行于y轴 |
16.截至2014年1月初,济南户籍总人口613.4万人,其中613.4万人用科学记数法表示为( )
| A. | 6.134×102人 | B. | 613.4×104人 | C. | 6.134×105人 | D. | 6.134×106人 |
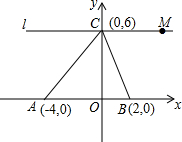 如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)
如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)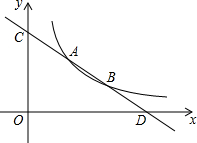 如图,点A(m,m+1),B(m+3,m-1)为第一象限内的点,并且都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,直线AB与y轴交于点C.
如图,点A(m,m+1),B(m+3,m-1)为第一象限内的点,并且都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,直线AB与y轴交于点C.