题目内容
14.已知二次函数y=kx2-4kx+3k(k≠0)(1)当k=1时,求该抛物线与坐标轴的交点的坐标;
(2)当0≤x≤3时,求y的最大值;
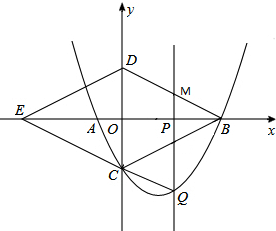
(3)若直线y=2k与二次函数的图象交于E、F两点,问线段EF的长度是否是定值?如果是,求出其长度;如果不是,请说明理由.
分析 (1)把k=1代入解析式,解一元二次方程得到答案;
(2)根据k>0和k<0两种情况,利用二次函数的性质解答即可;
(3)把直线y=2k与二次函数y=kx2-4kx+3k组成方程组,求出E、F的坐标,计算EF的长,得到答案.
解答 解:(1)当k=1时,该抛物线为:y=x2-4x+3,
x2-4x+3=0,
解得:x1=1,x2=3,
抛物线与x轴的交点的坐标为(1,0),(3,0),
当x=0时,y=3,
抛物线与y轴的交点的坐标为(0,3);
(2)对称轴为:x=-$\frac{b}{2a}$=-$\frac{-4k}{2k}$=2,
当k>0时,x=0时,y有最大值3k,
当k<0时,y的最大值即顶点的纵坐标,
为$\frac{4ac-{b}^{2}}{4a}$=-k,
(3)$\left\{\begin{array}{l}{y=k{x}^{2}-4kx+3k}\\{y=2k}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=2+\sqrt{3}}\\{{y}_{1}=2k}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2-\sqrt{3}}\\{{y}_{2}=2k}\end{array}\right.$,
E(2+$\sqrt{3}$,2k),F(2-$\sqrt{3}$,2k),
EF=2$\sqrt{3}$,
∴EF为定值.
点评 本题考查的是抛物线与x轴的交点的求法和二次函数的性质,掌握二次函数与一元二次方程的关系和二次函数的性质是解题的关键.

练习册系列答案
相关题目
3. 如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于( )
 如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于( )
如图,△ABC内接于半径为5的⊙O,圆心O到弦BC的距离等于3,则∠A的正切值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.当点P在线段AD上时速度是$\sqrt{5}$cm/s,在折线DE-EB上时速度是1cm/s.设点P的运动时间为t(s),且t>0,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD-DE-EB运动,到点B停止.当点P在线段AD上时速度是$\sqrt{5}$cm/s,在折线DE-EB上时速度是1cm/s.设点P的运动时间为t(s),且t>0,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上. 如图,在△BAC中,∠A=90°,∠B=60°,作AD⊥BC,垂足为D,E为边AB上一点,联结CE交AD于点P,点F为线段CE上一点,且CF:EF=3:1,联结FD.
如图,在△BAC中,∠A=90°,∠B=60°,作AD⊥BC,垂足为D,E为边AB上一点,联结CE交AD于点P,点F为线段CE上一点,且CF:EF=3:1,联结FD.
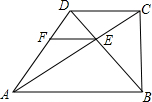 如图,直角梯形ABCD中,AB∥DC,∠ABC﹦90°,AD﹦BD,AC与BD相交于点E,AC⊥BD,过点E作EF∥AB交AD于F.
如图,直角梯形ABCD中,AB∥DC,∠ABC﹦90°,AD﹦BD,AC与BD相交于点E,AC⊥BD,过点E作EF∥AB交AD于F.