题目内容
18．
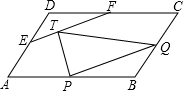如图，在?ABCD中，分别设P，Q，E，F为边AB，BC，AD，CD的中点，设T为线段EF的三等分点，则△PQT与?ABCD的面积之比是1：4．
分析 如图，连接AC、PE、QF．设平行四边形ABCD的面积为8S．只要证明四边形EFQP是平行四边形，求出平行四边形WFQP的面积，再求出△TPQ的面积即可解决问题．
解答 解：如图，连接AC、PE、QF．设平行四边形ABCD的面积为8S．
∵DE=AE，DF=FC，
∴EF∥AC，EF：AC=1：2，
∴S△DEF=$\frac{1}{4}$S△DAC=$\frac{1}{4}$×4S=S，
同理可证PQ∥AC，PQ：AC=1：2，S△CFQ=S△PQB=S△APE=S，
∴四边形EFQP是平行四边形，
∴S平行四边形EFQP=4S，
∴S△TPQ=$\frac{1}{2}$S平行四边形EFQP=2S，
∴S△TPQ：S平行四边形ABCD=2S：8S=1：4，
故答案为1：4．
点评 本题考查相似三角形的判定和性质、平行四边形的判定和性质、三角形的中位线定理等知识，解题的关键是学会添加常用辅助线，学会利用参数解决问题，属于中考常考题型．
练习册系列答案
小学课时特训系列答案
相关题目
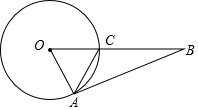如图，OA，OC都是⊙O的半径，点B在OC的延长线上，BA与⊙O相切于点A，连接AC，若AC=4，tan∠BAC=$\frac{2}{3}$，则⊙O的半径长为$\frac{4\sqrt{13}}{3}$．
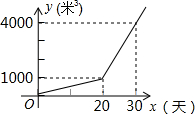某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系如图所示，当总用水量为2500米3时，该经济作物种植时间是25天．
10．下列各图象中，能反映y是x的函数的图象是（ ）
| A． |  | B． |  | C． |  | D． |  |