题目内容
8.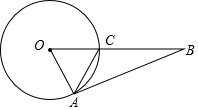 如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=4,tan∠BAC=$\frac{2}{3}$,则⊙O的半径长为$\frac{4\sqrt{13}}{3}$.
如图,OA,OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=4,tan∠BAC=$\frac{2}{3}$,则⊙O的半径长为$\frac{4\sqrt{13}}{3}$.
分析 作直径AD,连接CD,如图,利用圆周角定理得到∠ACD=90°,再根据切线的性质得∠DAB=90°,则利用等角的余角相等得到∠D=∠BAC,所以tanD=tan∠BAC=$\frac{3}{2}$,然后在Rt△ACD中利用正切定义可计算出CD=$\frac{8}{3}$,利用勾股定理可计算出直径AD的长.从而得到⊙O的半径.
解答 解:作直径AD,连接CD,如图,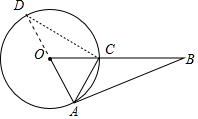
∵AD为直径,
∴∠ACD=90°,
∴∠D+∠DAC=90°,
∵BA与⊙O相切于点A,
∴OA⊥AB,
∴∠DAB=90°,即∠DAC+∠BAC=90°,
∴∠D=∠BAC,
∴tanD=tan∠BAC=$\frac{3}{2}$,
在Rt△ACD中,tanD=$\frac{AC}{CD}$,即$\frac{4}{CD}$=$\frac{3}{2}$,解得CD=$\frac{8}{3}$,
∴AD=$\sqrt{C{D}^{2}+A{C}^{2}}$=$\sqrt{(\frac{8}{3})^{2}+{4}^{2}}$=$\frac{4\sqrt{13}}{3}$,
∴⊙O的半径长为$\frac{4\sqrt{13}}{3}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了正切的定义.

练习册系列答案
相关题目
7.某校在选拔参加区运动会的同学,甲、乙、丙、丁四名同学在此前校运动会上掷铅球成绩的平均数与方差,如下表所示:
根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(m) | 12.4 | 13.7 | 13.6 | 12.9 |
| 方差 | 7.8 | 9.4 | 2.1 | 8.2 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
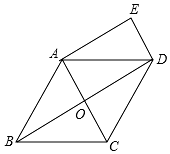 已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系?请说明理由.
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系?请说明理由.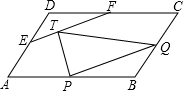 如图,在?ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与?ABCD的面积之比是1:4.
如图,在?ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与?ABCD的面积之比是1:4.