题目内容
16.(1)当x≤1时,化简:$\sqrt{{x}^{2}-2x+1}$-$\sqrt{{x}^{2}-4x+4}$;(2)$\frac{a-\sqrt{ab}}{\sqrt{a}-\sqrt{b}}$.
分析 (1)先根据完全平方公式公式变形,由范围判断x-1、x-2的符号,再根据二次根式和绝对值的性质计算;
(2)先分子$\sqrt{a}$,再根据分式的基本性质分子分母同时约去$\sqrt{a}$-$\sqrt{b}$即可求解.
解答 解:(1)∵x≤1,
∴$\sqrt{{x}^{2}-2x+1}$-$\sqrt{{x}^{2}-4x+4}$
=$\sqrt{(x-1)^{2}}$-$\sqrt{(x-2)^{2}}$
=1-x+x-2
=-1;
(2)$\frac{a-\sqrt{ab}}{\sqrt{a}-\sqrt{b}}$=$\frac{\sqrt{a}(\sqrt{a}-\sqrt{b})}{\sqrt{a}-\sqrt{b}}$=$\sqrt{a}$.
点评 考查了分母有理化,二次根式的性质与化简,(1)的关键是由范围判断x-1、x-2的符号.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
6. 如图,已知AB∥DE,则下列式子表示∠BCD的是( )
如图,已知AB∥DE,则下列式子表示∠BCD的是( )
 如图,已知AB∥DE,则下列式子表示∠BCD的是( )
如图,已知AB∥DE,则下列式子表示∠BCD的是( )| A. | ∠2-∠1 | B. | ∠1+∠2 | C. | 180°+∠1-∠2 | D. | 180°-∠2-2∠1 |
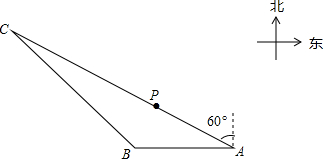 如图.有一艘渔船P在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从观测站A测得渔船P在北偏西60°的方向,同时测得搜救船C也在北偏西60°的方向,从观测站B测得渔船P在北偏东32°的方向,测得搜救船C在北偏西45°方向,已知观测站A在观测站B东40里处,问搜救船C与渔船P的距离是多少?(结果保留整数,参考数据:sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73).
如图.有一艘渔船P在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A,B上的观测点进行观测,从观测站A测得渔船P在北偏西60°的方向,同时测得搜救船C也在北偏西60°的方向,从观测站B测得渔船P在北偏东32°的方向,测得搜救船C在北偏西45°方向,已知观测站A在观测站B东40里处,问搜救船C与渔船P的距离是多少?(结果保留整数,参考数据:sin32°≈0.53,cos32°≈0.85;tan32°≈0.62,sin58°≈0.85;cos58°≈0.53;tan58°≈1.60;$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73). 如图,AB∥CD,NB、ND分别平分∠ABM和∠MDC,求证:∠M=2∠N.
如图,AB∥CD,NB、ND分别平分∠ABM和∠MDC,求证:∠M=2∠N. 如图,已知点P是直线AB外一点,按下列语句画出图形:
如图,已知点P是直线AB外一点,按下列语句画出图形: